2.1.1 Formulation générale

      Toute l'information que l'on peut obtenir sur un système constitué d'un ensemble de particules est contenue dans la fonction d'onde Y du système. La fonction d'onde d'un système composé de N atomes et 2n électrons est obtenue en résolvant l'équation de Schrödinger indépendante du temps suivante [1] :

      HY = EY (1)

      où E est l'énergie du système et H est l'opérateur correspondant : l'hamiltonien du système. Y est la fonction d'onde du système, fonction des coordonnées des noyaux, des électrons et contient toute l'information du système, E est l'énergie totale. Les valeurs propres de H sont les valeurs observables de cette énergie et les fonctions d'onde correspondantes sont les fonctions propres associées.

      Comme il l'a été dit au chapitre I, les propriétés moléculaires qui peuvent être calculées par la résolution de l'équation de Schrödinger sont la géométrie moléculaire, et donc les stabilités relatives, les spectres de vibrations, les moments dipolaires et quadripolaires, les spectres électroniques et aussi des fonctions descriptives de la réactivité, telles que les charges atomiques et les fonctions de Fukui. Toutefois, la précision avec laquelle on peut espérer calculer ces quantités est très variable en fonction de la nature de ces propriétés. Cette équation ne peut en effet pas être résolue de manière exacte pour les systèmes moléculaires, et l'on doit donc effectuer un certain nombre d'approximations.

      Pour un système traité comme étant composé de charges ponctuelles (2n électrons et N noyaux), sans traitement relativiste, l'hamiltonien pour un système à couches fermées est donné par :

      

       est la constante de Planck h divisée par 2p, m_e est la masse de l'électron, e est la charge de l'électron, M_A est la masse du noyau A, r_kA est la distance entre l'électron k et le noyau A, R_AB est la distance entre les noyaux de l'atome A et de l'atome B dont les charges nucléaires sont respectivement Z_A et Z_B. est le laplacien du k^ième électron défini de la manière suivante :

      

      Cet hamiltonien ne prend pas en considération les interactions entre les électrons et des champs extérieurs au système (par exemple RPE) ou entre les électrons et les spins nucléaires (par exemple RMN) ; elle est indépendante du temps.

      On constate que l'équation de Schrödinger, basée sur cet hamiltonien, est difficilement applicable à des molécules polyatomiques ; on doit donc introduire des approximations telles que l'approximation de Born-Oppenheimer et l'approximation orbitale pour la résoudre.

      On utilisera par la suite les notations en unité atomiques. Dans ce système d'unités m_e = 1 ; = 1, e = 1 et 4pe_o = 1. On assumera d'autre part que le système étudié est à couches fermées.

      Grâce à l'utilisation des unités atomiques, l'hamiltonien se simplifie sous la forme :

      

2.1.2 L'approximation de Born-Oppenheimer

      En 1927, Born et Oppenheimer ont proposé de simplifier la résolution de l'équation (1) en séparant la partie électronique de la partie nucléaire dans la fonction d'onde Y. Cette approximation est basée sur le fait que les électrons se déplacent beaucoup plus rapidement que les noyaux, ceci étant dû à la masse beaucoup plus faible des électrons (environ 1836 fois moindre de celle du proton). Par conséquent, les électrons réagissent quasi instantanément à une modification de la position des noyaux [2].

      En d'autres termes, pour une conformation R donnée des noyaux, seule la contribution électronique e(R) à l'énergie totale E est nécessaire pour connaître les propriétés du système. Cela revient donc à résoudre deux équations du type Schrödinger, l'une pour la partie nucléaire et l'autre pour la partie électronique. La fonction d'onde du système, solution de l'équation de Schrödinger dans l'approximation de Born et Oppenheimer, peut donc s'écrire sous la forme d'un produit de deux fonctions :

      

      où F(R) est la fonction d'onde nucléaire, Y_R(r) est la fonction d'onde électronique correspondant à un jeu de positions R des noyaux figés, r et R étant respectivement les positions des électrons et des noyaux.

      En écrivant l'hamiltonien H sous la forme :

      

      où V(r,R) est un potentiel dépendant de la position des électrons et des noyaux, on fait apparaître un opérateur électronique H_e(r;R) de la forme :

      

      On peut montrer, moyennant certaines approximations, que si l'on remplace l'expression (2) dans l'équation de Schrödinger, on obtient :

      

      la fonction d'onde Y_e(r) est une fonction propre de l'opérateur électronique H_e avec la valeur propre e(R), pour des positions R des noyaux figées. En résolvant l'équation (3) pour plusieurs positions successives des noyaux, on obtient alors une fonction de R :

      

      qui représente l'énergie Born-Oppenheimer du système en fonction des positions R des noyaux immobiles.

      Born et Oppenheimer ont aussi montré que le mouvement des atomes est régi par une équation de type Schrödinger où le potentiel dépend de l'énergie électronique évaluée par l'équation (3) :

      

      U(R) joue donc le rôle d'une énergie potentielle pour le mouvement des noyaux. L'ensemble des conformations R des atomes permet alors de construire une surface d'énergie potentielle appelée « surface de Born-Oppenheimer (BO) ». Il s'agira d'une fonction à 3N-6 variables (3N-5 pour les molécules linaires) dont les minima correspondent aux géométries stables de la molécule. Au minimum de plus basse énergie correspond la géométrie à l'équilibre de la molécule. La détermination de U(R) et de ses dérivées première et seconde permet de localiser des points stationnaires sur la surface de BO et, par conséquent, d'élaborer des chemins réactionnels. Elle donne aussi accès aux constantes de force des molécules et donc aux fréquences de vibrations, de même que peuvent être calculées des propriétés telles que le moment dipolaire, la polarisabilité, etc.

      Pour la résolution de la partie électronique, en considérant que le comportement des électrons n'est pratiquement pas modifié par les faibles déplacements des noyaux que l'on suppose comme étant figés dans leur position instantanée, l'hamiltonien dans l'approximation de Born-Oppenheimer se limite aux composantes électroniques seules :

      

      On remarque cependant que le dernier terme est un opérateur biélectronique alors que les deux premiers sont monoélectroniques, ce qui pose une difficulté ultérieure pour le traitement de la fonction Y_e.

2.1.3 L'approximation orbitale

      La fonction d'onde électronique Y_e (que nous désignerons dorénavant uniquement par la lettre Y) est une fonction des coordonnées de tous les électrons du système. Si 2n est le nombre d'électrons (2n est choisi ici par comodité), Y est une fonction à (2n)×3 variables que l'on note communément Y(1,2,... 2n).

      L'approximation orbitale, introduite par Hartree en 1928 [3], consiste à découpler les 2n électrons en développant la fonction Y(1,2,...,2n) en un produit de 2n fonctions monoélectroniques, de sorte que :

      

      où l'indice i désigne l'orbitale i

      Cette situation correspond physiquement à un modèle de particules indépendantes dans lequel chaque électron se déplace dans un champ moyen créé par les noyaux et la densité électronique moyenne des autres électrons. Cela signifie que chaque électron ressent les autres en moyenne, ce qui constitue naturellement une approximation.

      La fonction d'onde n'a cependant pas de terme décrivant le spin car celui-ci est absent de l'hamiltonien électronique. Pour décrire complètement la distribution des électrons, la coordonnée de spin s doit donc être introduite, et celle-ci prendra les valeurs +1/2 ou -1/2. Le spin est une propriété intrinsèque de l'électron, de nature purement quantique, et n'a donc pas d'équivalent en mécanique classique. La fonction d'onde de spin pour le spin aligné le long de l'axe (+)z sera a(s) et celle pour le spin aligné le long de (-)z sera b(s).

      La fonction d'onde électronique est donc composée d'une partie spatiale, l'orbitale, et d'une partie de spin. La fonction f est ce que l'on appelle une spin-orbitale et on l'écrit :

      f(r,s) = c(r)h(s)

      où r et s sont les coordonnées d'espace et de spin, respectivement.

      Pour un système à 2n électrons la fonction d'onde polyélectronique Y la plus simple s'écrira donc sous la forme d'un produit de spin-orbitales supposées normalisées :

      

      La fonction d'onde représentée par l'équation ci-dessus n'est cependant pas encore complète, car elle ne prend pas en compte l'indiscernabilité des électrons, ni le principe d'exlusion de Pauli [4]. Celui-ci a montré que pour les fermions (particules à spin ½), une spin-orbitale doit être antisymétrique par rapport à la permutation impaire des coordonnées d'espace et de spin. En permutant deux électrons il vient, par exemple :

      

      Une telle fonction obéit au principe d'exclusion de Pauli qui impose à deux électrons de ne pas pouvoir occuper la même spin-orbitale, ainsi qu'à l'indiscernabilité des électrons. Or, dans la formulation de Hartree de la fonction d'onde, cela n'est pas le cas, car l'électron i occupe précisément la spin-orbitale i.

      Hartree et Fock ont généralisé ce concept en montrant que le principe d'exclusion de Pauli est respecté si l'on écrit la fonction d'onde sous la forme d'un déterminant construit à partir de n spin-orbitales [5] ; on obtient alors ce qui est connu sous le nom de « déterminant de Slater » :

      

      Les variables x_i représentent ici les coordonnées d'espace et de spin. est le facteur de normalisation ; 2n étant le nombre d'électrons.

      On constate que la forme déterminantale de la fonction d'onde respecte le principe de Pauli : l'inversion de deux électrons correspond à la permutation de deux lignes (ou de deux colonnes), ce qui a pour effet de changer le signe du déterminant. Les spin-orbitales f_i  doivent, d'autre part, être différentes les unes des autres, car dans le cas contraire, le déterminant (6) s'annule.

      Le problème consiste dés lors à rechercher les meilleures spin-orbitales conférant l'énergie la plus basse possible au système, conformément au principe variationnel ; ce but est atteint un utilisant la méthode auto-cohérente de Hartee-Fock.

2.1.4 La méthode de Hartree-Fock

      Après avoir défini la forme de la fonction d'onde électronique globale d'un système polyélectronique à 2n électrons, il nous faut encore trouver l'expression de l'énergie électronique de ce système. D'autre part il nous reste à déterminer comment on peut obtenir les orbitales spatiales f_i servant à construire le déterminant de Slater ; celles-ci étant des orbitales moléculaires (construites sur une base de fonctions qui reste à déterminer) dans le cas des systèmes polyatomiques. L'énergie moyenne du système s'obtient aisément après quelques manipulations mathématiques sur l'expression générale (3) en utilisant une fonction d'onde Y de la forme Slater. On obtient alors une expression pour l'énergie électronique moyenne (où l'on somme sur les n orbitales électroniques) :

      

      où :

      

      Dans l'expression ci-dessus, le terme H_ii représente l'énergie d'un électron situé dans une orbitale moléculaire f_i placé dans le champ des noyaux ; ce terme est multiplié par deux car il y a 2 électrons par orbitales (pour un système à « couches fermées »).

      Les intégrales J_ij et K_ij sont respectivement appelées intégrales de Coulomb et intégrales d'échange ; l'intégrale de Coulomb a un équivalent en mécanique classique, alors que l'intégrale d'échange provient de la nécessité d'antisymétriser la fonction d'onde. Les intégrales de Coulomb et d'échange décrivent les interactions entre électrons. J_ij représente l'interaction coulombienne moyenne entre deux électrons situés dans les orbitales f_i et f_j, sans tenir compte de leur spin. L'intégrale d'échange K_ij réduit l'intéraction coulombienne entre deux électrons situés dans les orbitales f_i et f_j ayant des spins parallèles. Ce terme est une conséquence directe du principe de Pauli et conduit à une valeur d'énergie E_e plus basse, donc à une stabilisation. Par l'intermédiaire de l'intégrale d'échange on introduit ainsi une corrélation électronique entre électrons ayant des spins parallèles, c'est-à-dire que deux tels électrons ne peuvent pas se mouvoir indépendamment l'un de l'autre. On constate toutefois que ce modèle n'est pas apte à rendre compte de la corrélation entre électrons ayant des spins antiparallèles.

      Nous nous proposons maintenant de résoudre l'équation de Schrödinger électronique (3) avec une fonction d'onde Y qui a la forme d'un déterminant de Slater afin de trouver l'expression des fonctions f_i. Il est évident que ce déterminant ne peut pas être une solution exacte de l'équation de Schrödinger car une somme de termes monoélectroniques ne peut jamais être la solution d'une équation différentielle contenant des opérateurs biélectroniques. On doit, par conséquent, utiliser le principe variationnel [6].

      En utilisant cette idée, Fock et Slater ont développé de façon simultanée et indépendante ce qui est maintenant connu sous le nom d'équations de Hartree-Fock [7]. Le principe variationnel dit qu'étant donnée une fonction d'onde d'essai de la forme d'un déterminant de Slater, on peut montrer que l'on a toujours :

      

      où E₀ est l'énergie de la solution exacte . La « meilleure » fonction d'onde de type déterminant de Slater sera donc obtenue en faisant varier tous les paramètres qu'elle contient, jusqu'à ce que l'on obtienne l'énergie la plus basse. Cela revient à minimiser la quantité . En se rappelant qu'au cours de la minimisation, la fonction d'essai doit respecter la condition de normation , le problème revient alors à faire une minimisation avec contrainte que l'on résout par la méthode des « multiplicateurs de Lagrange ».

      Soit une fonction G dépendante de plusieurs fonctions inconnues telle que :

      

      où S_ij provient de la condition d'orthonormalité :

      e_ij sont les multiplicateurs de Lagrange supposés réels

      On a alors :

      

      et on obtiendra les points stationnaires de la fonction G, au premier odre, en résolvant l'équation :

      dG = 0

      La variation infinitésimale dG est obtenue en faisant varier d'une quantité infinitésimale chaque orbitale f_i, ce qui revient à remplacer f_i par f_i+df_i et f_j par f_j+df_j. On aura alors :

      

      Après quelques manipulations mathématiques, il est possible de se ramener à un système d'équations différentielles, les « équations de Hartree-Fock » :

      

      avec :

      

      h(1) est l'opérateur qui prend en compte l'énergie cinétique de l'électron 1 et son énergie potentielle d'interaction avec le noyau A. Les termes J et K ont été définis précédemment. Il faut encore noter que l'opérateur K est non-local car, comme le montre l'expression ci-dessus, il dépend de la valeur de f(1) sur tout l'espace.

      On constate ici que les opérateurs J et K s'expriment en fonction des solutions f de l'équation (8). On se trouve donc en présence d'un ensemble de N équations monoélectroniques non linéaires qu'il faudra résoudre par un processus itératif : à partir d'un jeu de spin-orbitales f_i d'essai on calcule l'opérateur

      

      pour en déduire ensuite un nouveau jeu de fonctions f_i. Ce processus est nommé auto-cohérent.

      Il est possible de montrer qu'il existe une transformation orthogonale des f_i amenant la matrice des multiplicateurs de Lagrande e_ij à sa forme diagonale. En appliquant cette transformation à nos orbitales f_i, on est apparemment conduit à un problème de valeurs propres puisque les équations (8) s'écrivent alors sous la forme :

      

      Ici e_i est l'énergie de l'orbitale i et F est l'opérateur monoélectronique de Fock donné par :

      

      Ce système d'équations ne prend en compte que les orbitales spatiales f_i. La seule référence au spin est faite lors du remplissage des orbitales où deux électrons seront placés par orbitale spatiale (principe de complémentarité appelé « aufbau »).

      Les équations de Hartree-Fock sont un jeu d'équations intégro-différentielles couplées, et ne peuvent être résolues que par une méthode itérative. Le couplage se constate par le fait que les intégrales J_ij et K_ij sont définies en fonction des orbitales f_i et f_j, ce qui veut dire que pour déterminer F(1) dans (10) on a besoin de connaître les autres orbitales f_j.

      Pour résoudre ces équations, un jeu d'orbitales d'essai est donc choisi : l'opérateur de Fock est ensuite construit et le système d'équations (9) est résolu de façon à obtenir un nouveau jeu d'orbitales. Cette procédure est appelée « méthode à champ auto cohérent » (SCF = Self Consistent Field), car les itérations sont continuées jusqu'à ce que le champ électrostatique ressenti par un électron (champ provoqué par les autres électrons dans les autres orbitales) reste stationnaire.

      Ces équations peuvent s'interpréter comme étant des équations de Schrödinger pour des électrons évoluant dans le champ des noyaux et des autres électrons du système, et dont les valeurs propres sont les énergies monoélectroniques e_i associées aux fonctions propres, les spin-orbitales. Il reste maintenant à expliciter la forme des spin-orbitales f_i pour résoudre les équations de Hartree-Fock.

2.1.5 L'approximation LCAO et les équations de Hartree-Fock-Roothaan

      Nous avons vu que les orbitales moléculaires optimales s'obtiennent en résolvant un ensemble d'équations différentielles non linéaires (ne pouvant être résolues rigoureusement que pour des atomes dans l'hypothèse d'une distribution électronique globale sphérique). Cette technique conduit à une tabulation des orbitales, ce qui les rend inadéquates pour un bon nombre d'applications. Si l'on désire obtenir des spin-orbitales moléculaires sous une forme analytique, on doit se résigner à résoudre de manière approchée les équations de Hartree-Fock en choisissant pour orbitales moléculaires des combinaisons linéaires d'orbitales atomiques.

      L'approximation LCAO proposée par Mulliken en 1941 [8] consiste à construire un jeu limité d'orbitales atomiques (OA) c_m qui constituera une base sur laquelle seront développées les orbitales moléculaires f_i (seule la partie spatiale des spin-orbitales est considérée ici). En essayant de résoudre les équations de Hartree-Fock pour des molécules, Hall, et indépendamment Roothaan, ont démontré qu'en introduisant un jeu de fonctions spatiales connues, les équations intégro-différentielles peuvent alors être transformées en un système d'équations algébriques et ainsi être résolues en utilisant la méthode habituelle des matrices [9]. Les nouvelles équations que l'on obtient dans cette approximation sont les équations de Hartree-Fock-Roothan.

      Si l'on considère un ensemble de m orbitales atomiques (c_l,c_m,c_n,c_r, ...) servant de base au développement des m orbitales moléculaires f_i(r) d'un système à couches fermées comportant 2n électrons, les orbitales moléculaires seront exprimées comme une combinaison linéaire de ces m fonctions spatiales mono-électroniques atomiques :

      

      Les c_mi sont les coefficients des orbitales moléculaires développées sur les fonctions de base. En toute rigueur le développement devrait être infini. Dans la pratique, il est clairement impossible de construire une base infinie d'orbitales. Par convention les OA sont centrées sur les atomes (d'où leur nom) et le symbole m correspond à l'atome sur lequel se trouve l'orbitale c. Il faut encore remarquer que malgré le terme « d'orbitales atomiques », celles-ci ne sont pas toujours les orbitales auto-cohérentes de l'atome isolé. Par cette méthode, les orbitales f_i sont délocalisées sur l'ensemble de la molécule et pour cette raison elles s'appelleront « orbitales moléculaires ». La terminologie généralement admise pour désigner des orbitales moléculaires (OM) obtenues par l'optimisation des coefficients des fonctions de base atomiques qui sont des combinaison linéaires d'orbitales atomiques (LCAO) est LCAO-MO. Les orbitales moléculaires doivent, en outre, respecter les conditions de normation et d'othogonalité mutuelle que l'on écrit :

      

      où d_ij est le symbole de Kronecker et S_mn est communément appelée intégrale de recouvrement des orbitales c_m et c_n, et s'écrit :

      

      Ce développement, appliqué aux équations de Hartree-Fock, conduit aux équations de Hartree-Fock-Roothan auxquelles on applique une fois encore le principe variationnel : on minimise l'énergie totale e par rapport aux coefficients du développement et l'on obtient alors les équations :

      

      i = 1,2,...m étant les coefficients des orbitales moléculaires, et m = 1,2,...,m étant les coefficients des orbitales atomiques. On aura les termes suivants :

      

      et est la matrice de population pour ce système à couches fermées.

      Le choix de la base constituée par les orbitales atomiques c_m est fondamental, car il joue un rôle important, tant sur la précision des résultats, que sur les temps de calculs nécessaires pour les obtenir, comme il sera vu plus loin dans ce chapitre.

      La résolution de ce système d'équations passe par l'annulation d'un déterminant construit sur les m équations à m+1 inconnues (les coefficients C_mi et les e_i relatifs), ce qui conduit à l'équation séculaire du système étudié :

      

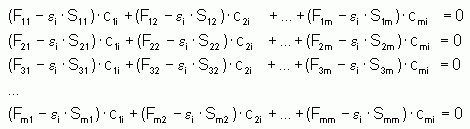
      Sa résolution consiste alors à développer ce déterminant et à en trouver les racines (les e_i) qui l'annulent. Chaque racine sera ensuite injectée à tour de rôle dans les équations de Hartree-Fock-Roothaan afin d'en obtenir les coefficients C_mi :

      

      Le système n'est linéaire qu'en apparence car les éléments de matrice F_mn sont quadratiques dans les C_mi. Toutefois, pour pouvoir le résoudre on suppose qu'il est linéaire et on travaille de façon auto-cohérente. On remarque aussi que contrairement aux équations intégro-différentielles de Hartree-Fock, le système d'équations (12) est un système d'équations algébriques. Elles peuvent donc se ramener à l'équation séculaire, écrite dans sa forme générale déterminantale :

      

      qui peut aussi s'écrire sous la forme matricielle suivante :

      FC = SCE (13)

      Les programmes de calculs travaillent généralement sous forme matricielle, ce qui évite de devoir résoudre des équations du nième degré (où n est le nombre de fonctions de base); ces équations, après transformation orthogonale, deviennent alors :

      

      ce qui n'est rien d'autre qu'une équation aux valeurs propres et vecteurs propres, facilement résolvable par les ordinateurs. C est une matrice carrée des coefficients du développement et E est le vecteur des énergies.

      

      L'équation ci-dessus est résolue d'une manière analogue à la résolution des équations de Hartree-Fock. Un premier essai est fait en utilisant des valeurs approchées pour les coefficients C_mi, la matrice de Fock est construite, puis elle est diagonalisée pour obtenir de nouveaux coefficients et de nouvelles énergies. Les nouveaux coefficients sont ensuite utilisés pour construire une nouvelle matrice de Fock et la procédure est répétée jusqu'à convergence des énergies ou des coefficients (dont le seuil est à fixer). L'énergie totale du système sera ensuite donnée par l'équation :

      

      avec les éléments P_mn et H_mn précédemment définis.

      Pour terminer, il faut encore remarquer que comme l'opérateur F est construit à partir de fonctions d'onde qui sont des approximations de celles de Hartree-Fock, il ne peut constituer qu'une forme approchée de l'hamiltonien de Hartree-Fock ; le système d'équations de Hartree-Fock-Roothaan ne constitue donc qu'une approximation des « vraies » équations de Hartree-Fock. La terminologie, « énergie Hartree-Fock » pour désigner le résultat de ces équations est donc abusive. En effet, si la base des OA était infinie, l'énergie E serait l'énergie de Hartree-Fock exacte, mais il n'en est rien. Les orbitales moléculaires obtenues dans l'approximation LCAO-MO ne sont donc que des approximations de celles de Hartree-Fock. Par convention, cependant, et sauf indication explicite, l'énergie issue du traitement Roothaan est appelée « énergie Hartree-Fock ».

2.1.6 Les fonctions de base utilisées dans l'approximation LCAO-MO

      Comme il l'a été dit, le choix de la base de fonctions représentant les orbitales atomiques est important car il peut influencer tant la précision des résultats obtenus que les temps de calculs.

      On distingue plusieurs types de bases d'orbitales atomiques : pour les bases minimales on choisit pour orbitales atomiques celles qui sont effectivement occupées à l'état fondamental du système en y ajoutant les orbitales inoccupées de la couche de valence. Chaque orbitale c_m n'est décrite que par une seule fonction (la fonction 1s de l'hydrogène, par exemple).

      Les bases étendues sont composées de la base minimale, où chaque orbitale est décrite par deux fonctions, à laquelle sont ajoutées un certain nombre d'orbitales situées au-delà de la couche de valence des différents atomes; celles-ci sont appelées orbitales de polarisation (pour l'hydrogène: 1s, 1s', 2p_x, 2p_y et 2p_z).

      Les bases de valence ne comprennent quant à elles que les orbitales de la couche de valence de chaque atome et en général une seule fonction de base par orbitale. Les électrons des couches internes (dits électrons de coeur) ne sont pas décrits explicitement dans ce type de base, mais un potentiel reproduit leur effet.

      Il semblerait naturel d'utiliser, comme orbitales atomiques, des fonctions de Hartree-Fock obtenues en résolvant l'équation du champ auto-cohérent pour les atomes libres. Leur défaut essentiel est de ne pas posséder de forme analytique, de sorte que le calcul des intégrales moléculaires est considérablement alourdi. Pour ces raisons, on a préféré, historiquement, la base de fonctions de Slater, qui sont de bonnes approximations des orbitales de Hartree et qui s'écrivent dans leur forme générale [10] :

      

      (n,l,m) sont les nombres quantiques principal, azimutal et magnétique, (r,q,f) sont les coordonnées sphériques définissant la position de l'électron, a est une constante déterminée à l'aide de règles empiriques, visant à reproduire au mieux le comportement des orbitales hydrogénoïdes, et U_i,m(q,f) sont les harmoniques sphériques des parties angulaires des solutions de l'équation de Schrödinger pour les atomes de type hydrogénoïdes.

      Par rapport aux parties radiales hydrogénoïdes qui sont de meilleures solutions du problème atomique, les fonctions de Slater ont le désavantage de ne pas avoir de noeuds radiaux et, pour toutes celles de type s (sauf la 1s), d'être nulles à l'origine, ce qui n'est pas le cas des hydrogénoïdes. On résout pratiquement ces difficultés en utilisant le plus souvent des combinaisons linéaires de fonctions de Slater comme fonctions de bases atomiques, ce qui permet d'obtenir des représentations précises des orbitales atomiques de Hartree-Fock-Roothaan. Toutefois, si l'on construit une base LCAO de ce type pour un calcul moléculaire, le calcul des intégrales biélectroniques sera particulièrement difficile. La raison en est que le produit de deux orbitales de Slater situées sur des centres différents ne peut être exprimé simplement par une seule fonction. On préfère donc en général utiliser des fonctions de Gauss cartésiennes. Ces fonctions, proposées par Boys [11], sont des puissances de x,y,z multiplié par , a étant une constante déterminant l'extension radiale de la fonction :

      

      où i,j,k sont des nombres entiers simulant les nombres quantiques n,l,m. N est le facteur de normalisation et x est l'exposant de la gaussienne.

      Par exemple :

      

      Les gaussiennes sont des fonctions très populaires en chimie quantique, spécialement pour les méthodes ab initio, car le produit de deux gaussiennes centrées sur deux atomes A et B différents peut s'écrire à l'aide d'une seule gaussienne centrée en un point situé sur le segment AB. Le calcul des intégrales biélectroniques en ressort ainsi considérablement simplifié.

      Bien que les fonctions de Slater soient peu commodes d'utilisation pour les calculs numériques, elles présentent l'avantage de décrire raisonnablement les orbitales atomiques. Les bases gaussiennes ont, par contre, une assez mauvaise représentation des orbitales atomiques car elles n'ont pas un comportement exact à l'origine (dérivée devant être nulle), ni aux grandes distances (décroissance trop rapide avec r). Pour compenser la représentation incomplète des orbitales atomiques des fonctions gaussiennes, on utilise donc des combinaisons linéaires de gaussiennes comme fonctions de base. Ces fonctions sont appelées « fonctions gaussiennes contractées ». Il faut en général utiliser trois fonctions gaussiennes pour que l'ajustement des parties radiales soit satisfaisant. On aura par exemple :

      

      où d₁, d₂, d₃ sont les coefficients fixes de cette combinaison linéaire appelée « STO-3G ».

      Il existe bon nombre de bases de gaussiennes possibles. Les plus communément utilisées sont celles qui ont été développées par Pople et collaborateurs [12]. La plus simple est la base STO-3G, aussi appelée « base minimale ». Le sigle « 3G » signifie que les orbitales de type Slater (STO) sont représentées par trois fonctions gaussiennes. Le niveau suivant développé par Pople comprend les bases split-valence telles que 3-21G, 4-31G et 6-31G, où le premier chiffre représente le nombre de gaussiennes utilisées pour représenter les orbitales de coeur. Les orbitales de valence y sont représentées par deux fonctions qui sont composées du nombre de gaussiennes indiqué dans la seconde partie de la dénomination de la base. Ainsi la base 6-31G du carbone, par exemple, utilisera six gaussiennes pour représenter l'orbitale 1s, trois gaussiennes pour l'orbitale 2s et 1 gaussienne pour représenter les orbitales 2p.

      Pour une plus grande flexibilité on peut encore rajouter des fonctions de polarisation. La dénomination la plus ancienne est l'ajout d'un astérisque sur la base en question (par exemple 6-31G*), et dans une désignation plus récente, le caractère de la fonction ajoutée est explicitement donné : 6-31G(d). La base 6-31G* ou 6-31G(d) signifie ainsi qu'un jeu de fonctions d a été ajouté à tous les atomes (sauf H) dans la molécule, alors que 6-31G** ou 6-31G(p,d) signifie qu'un jeu de fonctions p a été ajouté aux hydrogènes et que des fonctions d ont été ajoutées aux autres atomes.

---

2.1.7 Les méthodes de calculs utilisant l'approche Hartree-Fock

      Les nombreuses méthodes de calculs fondées sur l'approximation de Hartree-Fock utilisent généralement l'approximation LCAO-MO comme point de départ. Les méthodes non-empiriques (ou ab initio) effectuent une résolution rigoureuse de ces équations en calculant toutes les intégrales à deux électrons. Les méthodes semi-empiriques négligent quant à elles un grand nombre de ces intégrales, et calculent les autres de manière approchée en faisant intervenir des paramètres ajustables déterminés empiriquement.

2.1.8 Le traitement de la corrélation électronique : les méthodes post Hartree-Fock

      L'énergie Roothaan est égale à l'énergie Hartree-Fock dans le cas où la base de fonctions utilisée est infinie. Dans la théorie Hartree-Fock, l'énergie la plus basse pouvant être obtenue est E_HF, c'est la limite Hartree-Fock. Or, cette théorie est approximative ; elle néglige, comme il l'a été dit, l'énergie de corrélation des électrons. Les électrons de spin opposés (particulièrement ceux situés dans des orbitales ayant des parties spatiales similaires) exercent, en effet, les uns sur les autres des forces répulsives dépendant de leurs positions instantanées. Or, dans le modèle des particules indépendantes de Hartree-Fock, cet effet est en partie négligé puisque l'on suppose que chaque électron se trouve dans le champ moyen crée par tous les autres. La contribution à l'énergie totale de cette interaction interélectronique d'origine quantique est faible, mais elle devient importante lorsque de petites différences d'énergie doivent être calculées.

      D'après Löwdin [13], l'énergie de corrélation d'un système correspond à la différence entre l'énergie Hartree-Fock et l'énergie exacte non-relativiste du système :

      

      Le modèle Hartree-Fock est certes très utile pour prédire certaines propriétés atomiques ou moléculaires, mais les méthodes post Hartree-Fock sont parfois nécessaires pour retrouver l'énergie de corrélation, car un traitement de la corrélation électronique plus poussé peut se révéler essentiel pour l'obtention de certaines propriétés atomiques ou moléculaires. La recherche des fonctions d'onde sera donc rendue plus compliquée, et pour ce faire, plusieurs méthodes ont été proposées, comme il l'a déjà été mentionné en introduction au chapitre I. Deux grandes catégories de méthodes existent actuellement : les méthodes à référence unique et les méthodes multiréférencées.

      La fonction d'onde HF ne décrit pas correctement le comportement des électrons à proximité du noyau et surestime la probabilité de trouver deux électrons proches l'un de l'autre. Ces effets de corrélation à courte distance sont dus au trou de Coulomb [14] et l'énergie de corrélation qui en découle est appelée, comme déjà dit, « corrélation dynamique ». Les effets de corrélation à longue distance contribuent, quant à eux, à l'énergie de « corrélation non dynamique » (ou statique) et à cause de ces effets, les calculs HF ont tendance à sous-estimer les longueurs de liaison. Lorsque ces effets sont faibles, la fonction d'onde HF fournit une bonne description du système et pour récupérer l'énergie de corrélation, des méthodes post-HF basées sur une référence unique suffisent.

      Par chance, cette situation est la plus répandue (systèmes à l'état fondamental proche de l'équilibre) ; par contre, dans les autres situations, la description mono-déterminantale de la théorie HF est insuffisante (états excités, molécules proches de la dissociation ou états électroniquement quasi-dégénérés). Dés lors il faut utiliser des méthodes post-HF multiréférencées (MCSCF, MRCI) qui ne seront pas décrites ici.

---

2.2.1 Fondements de la théorie

      La théorie de la fonctionnelle de la densité est basée sur le postulat proposé par Thomas et Fermi qui dit que les propriétés électroniques peuvent être décrites en terme de fonctionnelles de la densité électronique, en appliquant localement des relations appropriées à un système électronique homogène [15]. Thomas et Fermi ont utilisé leur théorie pour la description d'atomes, mais le manque de précision, ainsi que l'impossibilité de traiter des systèmes moléculaires en ont fait un modèle trop simpliste lorsqu'il a été proposé.

      Hohenberg et Kohn, en 1964 [16], ont repris la théorie de Thomas-Fermi et ont montré qu'il existe une fonctionnelle de l'énergie E[r(r)] associée à un principe variationnel, ce qui a permis de jeter les bases de la théorie de la fonctionnelle de la densité. Des applications pratiques ont ensuite été possibles grâce aux travaux de Kohn et Sham (KS) [17] qui ont proposé, en 1965, un set d'équations monoélectroniques analogues aux équations de Hartree-Fock à partir desquelles il est en principe possible d'obtenir la densité électronique d'un système et donc son énergie totale.

      Fonctionnelle et dérivée fonctionnelle sont des entités mathématiques de première importance dans la théorie DFT. Mathématiquement, on désigne par « fonctionnelle » une entité qui fait correspondre un nombre à chaque fonction provenant d'une classe définie. En d'autres termes, c'est une fonction de fonction. La notation d'une fonctionnelle est F[f(r)], où r est une variable de la fonction f. La dérivée fonctionnelle est la quantité telle que :

      

      L'équation (15) représente la série coupée jusqu'au terme linéaire de dr. Comme il va l'être vu plus avant, il existe une correspondance biunivoque entre la densité électronique d'un système et le potentiel externe v(r). La densité électronique r(r) constitue la grandeur fondamentale de la DFT, et les termes de l'hamiltonien électronique (4) utilisé en début de ce chapitre peuvent s'écrire en fonction de matrices densité, grandeurs qui généralisent la notion de densité électronique.

      La densité électronique r(r₁) de l'électron 1, de coordonnées r₁, est en fait l'élément diagonal d'une matrice densité  ¹  r₁(r₁',r₁). Si y est la spin-orbitale donnant la densité r(r₁), on peut alors calculer r(r₁) d'après l'expression :

      

      où les s_i sont les coordonnées de spin et les r_i sont les coordonnées d'espace. r₁ est donc une « matrice densité d'ordre 1 » [25].

      De la même manière, on défini une « matrice densité d'ordre 2 » r₂(r₁'r₂', r₁r₂) dont l'élément de matrice diagonal est r₂(r₁r₂,r₁r₂) = r₂(r₁r₂) et dont l'expression est :

      

      Il est important de noter que l'intégrale sur tout l'espace de r(r₁) donne le nombre d'électrons N total du système, tandis que la matrice densité d'ordre 2 intègre sur le nombre de paires d'électrons

      Plus généralement, on peut construire une matrice que nous appellerons matrice densité d'ordre p, et telle que :

      

      où correspond au coefficient binômial.

      Dans le cadre de la description des propriétés régies par des intéractions interélectroniques, les matrices densité d'ordre 1 et 2 suffisent.

      Avec ces nouvelles grandeurs il est maintenant possible de réécrire chacun des composants d'énergie provenant de l'hamiltonien (4) :

      

      On constate que le terme V_ee[r] est composé de deux parties; la première correspond à l'interaction coulombienne classique J[r], et la seconde partie dite non-classique est appelée « énergie d'échange et de corrélation ».

2.2.2 Les théorèmes de Hohenberg et Kohn

      Les deux théorèmes de Hohenberg et Kohn formulés en 1964 [16] ont permis de donner une cohérence aux modèles développés sur la base de la théorie proposée par Thomas et Fermi à la fin des années 30.

---

---

---

2.2.3 La méthodologie de Kohn-Sham

      La fonctionnelle de Hohenberg et Kohn contient une composante d'énergie cinétique T[r] et une composante d'énergie potentielle V_ee[r]. Cette dernière peut, comme il l'a déjà été dit, elle-même se scinder en une partie classique (la répulsion coulombienne), notée J[r], et une partie d'origine quantique, K[r]. Thomas et Fermi avaient proposé une approximation de T[r], mais celle-ci, comme il l'a été dit, s'est révélée être insuffisante pour décrire de manière satisfaisante l'énergie cinétique des systèmes électroniques. Kohn et Sham ont proposé en 1965 [17] de calculer une énergie cinétique approchéeT_s[r] en introduisant les orbitales.

      Cette méthode, plus indirecte, est donc basée sur l'utilisation d'orbitales qui permettent d'évaluer avec une bonne précision l'énergie cinétique ; une faible correction étant apportée dans un second temps. La formulation exacte de l'énergie cinétique pour l'état fondamental est la suivante :

      

      où les y_i sont les spin-orbitales naturelles du système et n_i est leur nombre d'occupation respectif. Le principe de Pauli impose la condition 0 Ł n_i Ł 1 et selon la théorie de Hohenberg-Kohn, l'énergie cinétique T est une fonctionnelle de la densité électronique totale donnée par :

      

      Pour un système où les électrons sont sujets à des interactions, il y a néanmoins un nombre infini de termes dans les expressions de T et de r.

      Ces équations correspondent en fait au cas où n_i = 1 pour N orbitales, et n_i = 0 pour le reste. Cette condition n'est valable que pour les fonctions d'onde déterminantales décrivant un système à N électrons sans interactions. Afin d'avoir une unique décomposition en termes d'orbitales conduisant à une seule valeur exacte pour T_S[r], Kohn et Sham ont proposé, par analogie avec la définition de la fonctionnelle universelle de Hohenberg et Kohn, un système de référence sans interactions, et l'énergie cinétique est calculée selon l'expression :

       pour les N orbitales

      la quantité T[r]-T_s[r] étant cependant faible.

      A priori T_s[r] n'est pas l'énergie cinétique du système étudié ; Kohn et Sham ont reformulé le problème de manière à ce que le système de référence d'électrons non-intéragissant ait la même densité électronique que l'état fondamental du système étudié. Pour cela, ils ont réécrit la fonctionnelle F[r] de la manière suivante :

      F[r] = T_s[r] + J[r] + E_xc[r]

      avec :

      E_xc[r] = T[r] - T_s[r] + V_ee[r] - J[r]

      La quantité E_xc[r] est appelée « énergie d'échange-corrélation ». L'équation (21) devient alors :

      

      avec le potentiel effectif V_eff :

      

      où v_xc est le potentiel d'échange-corrélation, dérivée fonctionnelle de E_xc[r] par rapport à r(r). L'équation (22) est exactement la même que celle de la théorie de Hohenberg et Kohn pour un système d'électrons non-intéragissant se déplaçant dans un potentiel effectif de la forme de v_eff(r).

      En appliquant le principe variationnel, on obtient alors un ensemble d'équations du type Hartree-Fock que l'on résout par un processus intératif :

      

      La densité électronique est ensuite obtenue par la sommation :

      

      Pratiquement, on choisit une densité d'essai à partir de laquelle on calcule un potentiel effectif v_eff(r). En injectant v_eff(r) dans l'expression (23) on obtient une nouvelle densité électronique (24). La convergence est alors atteinte lorsque le potentiel effectif ne varie plus.

      Ces équations sont analogues à celles obtenues par la méthode de Hartree-Fock, mais contiennent un potentiel local plus général V_eff(r). Les théories quantiques vues dans ce chapitre (Hartree, Hartree-Fock et Kohn-Sham) conduisent toutes à un système d'équations mono-électroniques, mais le formalisme de Kohn-Sham permet néanmoins de tenir compte, de manière intrinsèque, de l'effet dû à l'échange et à la corrélation électronique.

      Il faut encore ajouter que le terme V_eff(r) ne contient pas d'opérateur de spin, et chaque solution pour e_i est doublement dégénérée ; on a donc les deux cas suivants :

      

      Pour le cas « closed-shell », on aura :

      

      Pour un système à couches ouvertes, on aura par contre :

      

      Cette condition de restriction découle directement de la théorie, alors que dans le cas Hartree-Fock elle était la conséquence de l'approximation orbitale de Hartree. Il faut noter que les orbitales utilisées dans l'équation de Kohn-Sham sont celles conduisant à un minimum pour l'énergie totale et sont obtenues de manière auto-cohérente. La signification physique de ces orbitales n'est cependant pas claire ; l'orbitale HOMO permet néanmoins d'obtenir la valeur du potentiel d'ionisation, sur la base du théorème de Janak.

      Kohn et Sham ont donc permis à la DFT de devenir un outil efficace pour l'étude des systèmes chimiques. Actuellement, la très grande majorité des calculs DFT sont réalisés dans le cadre de ce formalisme ; les approximations qui vont brièvement être décrites ci-après s'inscrivent dans le cadre du formalisme de Kohn-Sham.

2.2.4 L'approximation locale LDA

      La difficulté principale dans le développement du formalisme de Kohn-Sham réside dans la construction des fonctionnelles d'échange-corrélation. L'approximation locale dite « LDA » stipule qu'en première approximation la densité peut être considérée comme étant localement constante. On peut dés lors définir l'énergie d'échange-corrélation de la manière suivante :

      

      où e_xc(r) est la densité d'énergie d'échange-corrélation.

      Cette approximation découle directement du modèle du gaz homogène d'électrons. Par ailleurs, si l'on partitionne l'énergie d'échange-corrélation en deux (énergie d'échange e_x et énergie de corrélation e_c) telle que :

      e_xc = e_x + e_c

      on peut utiliser l'énergie d'échange proposée par Dirac [26] comme approximation de e_x :

      

      La fonctionnelle de corrélation la plus utilisée a été développée par Vosko, Wilk et Nusair en 1980 [27]. Ces auteurs ont utilisé les résultats de calculs Monte Carlo effectués par Ceperley et Alder pour ajuster une expression analytique de l'énergie de corrélation. Cette fonctionnelle est connue sous l'abréviation « VWN ».

      Dans la pratique, la méthode LDA se montre plus performante que les calculs Hartree-Fock. On constate cependant qu'en général cette approximation a tendance à raccourcir les longueurs de liaison dans les molécules et, par conséquent, à surestimer les énergies de liaison. De plus, il est très fréquent que les barrières d'activation des réactions chimiques soient largement sous-estimées. Les fréquences de vibration sont par contre généralement en bon accord avec l'expérience (l'écart étant souvent inférieur à 5 %).

      Depuis 1985 d'énormes efforts ont contribué à l'amélioration des fonctionnelles d'échange-corrélation. Ces travaux ont débouché sur une deuxième génération de fonctionnelles incluant l'inhomogénéité de la densité électronique : ces fonctionnelles prennent donc en compte la densité électronique ainsi que son gradient.

2.2.5 L'approximation des gradients généralisés GGA

      La densité électronique d'un système est non seulement pas uniforme, mais peut même varier très rapidement dans l'espace (lorsqu'on passe d'une couche électronique à l'autre dans un atome, ou lorsqu'on passe d'un atome à l'autre dans une molécule). La première amélioration que l'on puisse apporter à la méthode LDA consiste donc à exprimer la fonctionnelle d'énergie d'échange-corrélation en fonction de la densité électronique et de son gradient.

      Cette technique est appelée « approximation de l'expansion du gradient » (GEA). Elle se révèle efficace pour les systèmes dont la densité électronique ne varie que lentement. Pour les systèmes chimiques, il s'avère qu'elle donne des résultats moins bons que LDA. La solution consiste alors à réécrire l'expression d'échange-corrélation sous une forme similaire à LDA :

      

      où e_xc^GGA est la densité d'énergie d'échange-corrélation. La difficulté réside dés lors dans la recherche d'expressions analytiques de e_xc^GGA.

      De nombreuses fonctionnelles ont été developpées depuis, tant pour l'échange que pour la corrélation. Parmi les plus connues et les plus utilisées on peut citer les fonctionnelles d'échange de Becke (B88) [28] et de Perdew et Wang (PW91) [29]. Pour la corrélation, on dispose, entre autres, des fonctionnelles de Perdew (P86) [30], de Lee, Yang et Parr (LYP) [31] et de Perdew et Wang (PW91) [29]. Toutes ces fonctionnelles permettent une amélioration de l'estimation des énergies de liaison dans les molécules, ainsi que des barrières d'énergie par rapport à l'approximation locale LDA.

      Il faut encore citer les fonctionnelles dites « hybrides », basées sur le formalisme de la connection adiabatique [32]. Le principe émerge de la question demandant s'il est possible d'utiliser l'échange de Hartree-Fock dans le formalisme de Kohn-Sham. La formule de la connection adiabatique justifie théoriquement la détermination de l'énergie d'échange HF à partir de l'énergie des orbitales Kohn-Sham. L'utilisation de la partie d'échange HF associée aux fonctionnelles GGA fournit des résultats comparables à ceux de l'approximation des gradients généralisés. La première fonctionnelle de ce type a été proposée par Becke, et contient 50 % d'échange HF ; c'est la fonctionnelle « half and half » [33]. Elle présentait l'inconvénient de contenir une trop forte proportion d'échange HF, et la fonctionnelle de ce type actuellement la plus utilisée est celle connue sous l'acronyme B3LYP [34]. Celle-ci est une fonctionnelle à trois paramètres combinant les fonctionnelles d'échange local, d'échange de Becke et d'échange HF, avec les fonctionnelles de corrélation locale (VWN) et corrigée du gradient de Lee, Yang et Parr.

      Enfin, de nouveaux travaux ont récemment été entrepris afin de développer de nouvelles fonctionnelles ab initio sans paramètres. A l'heure actuelle, il n'existe qu'une seule fonctionnelle de ce type, élaborée par Perdew, Burke et Ernzerhof (PBE) [35], qui s'est montrée très efficace pour les calculs de géométries, de fréquences et d'énergies d'excitations électroniques.

2.2.6 Conclusion

      Les développements théoriques ont permis de faire de la physique quantique appliquée à la chimie un outil indispensable associé à la chimie expérimentale.

      Nous avons eu ainsi moyen, dans ce chapitre, de constater qu'au cours des années de développement de la chimie quantique deux voies se sont dégagées ; l'une aborde les problèmes en décrivant les systèmes par une fonction d'onde, l'autre le fait par le biais de sa densité électronique.

      Les méthodes DFT souffrent cependant d'un manque de procédures systématiques qui permettent d'améliorer les fonctionnelles et les propriétés moléculaires calculées, ce qui n'est pas le cas avec les calculs ab initio pour lesquels il est à priori possible d'augmenter la qualité des résultats en augmentant le niveau de calculs ou la qualité de la base de fonctions. La seule limitation dans le cas ab initio étant naturellement liée au temps requis pour effectuer de tels calculs.

      Il a été vu que ces deux méthodes peuvent parfois être utilisées conjointement, et il ne serait pas si surprenant que dans un futur proche, ces deux théories donnent naissance à une nouvelle théorie mixte dans laquelle la fonctionnelle d'énergie serait orbitalairement dépendante et non plus densité-dépendante [36].

2.3.1 La méthode du « continuum solvation »

      La possibilité d'intégrer les effets dus au solvant pour le calcul des différentes propriétés des systèmes chimiques reste un challenge dans la chimie quantique, car cela implique l'intervention de la mécanique statistique et donc, l'ajout de difficultés d'ordre supérieur. La majorité des réactions chimiques et biologiques ont cependant lieu en solution, et le désir du chimiste théorique est donc celui de pouvoir posséder et utiliser des modèles permettant de tenir compte des effets dus au solvant.

      Tomasi et Persico [42,45-46] ont proposé de diviser les différentes approches possibles du traitement des effets de solvant en quatre catégories :

• Equation d'état virielle, fonctions de corrélation
• Simulation de type Monte Carlo ou de dynamique moléculaire
• Traitements de type continuum
• Traitements moléculaires

      La partie de théorie présentée ci-après ne se veut être qu'une introduction des différentes méthodes de solvatation ; pour plus de détails, l'excellent article de Tomasi et Persico [46] les passe en revue, tout en présentant les éléments mathématiques absents ici.

      L'idée de modéliser les interactions électrostatiques dues au solvant en plaçant le soluté dans une cavité de taille définie date des travaux de Kirkwood [43] et Onsager sur les effets de solvatation sur les molécules polaires [44]. A partir de l'équation de Laplace (ou de Poisson), et sous certaines conditions limites, plusieurs modèles ont été par la suite proposés [41-50]. Dans cette approche, le soluté, traité de manière quantique, est placé dans une cavité entourée de molécules de solvant considérées comme un continuum. Ce modèle de continuum simple est le « modèle de la cavité d'Onsager », souvent dénommé « modèle SCRF », pour « Self-Consistent Reaction Field ».

      Les modèles de type « continuum » impliquent toutes sortes de formes de cavité contenant le soluté, et le solvant se trouvant en-dehors est traité comme un milieu continu, caractérisé par quelques-unes seulement de ses propriétés comme sa constante diélectrique, par exemple. Le champ électrique produit par les particules chargées comprenant le soluté interagit alors avec ce milieu, produisant une polarisation, ce qui se reflète sur les fonctions d'onde du soluté.

      La cavité représente la portion de l'espace où la densité de solvant est nulle et où le soluté prend place. Il est bien connu que la réponse d'un milieu diélectrique continu à toute distribution de charge consiste en une distribution de charge de surface à l'interface entre les deux. Le problème, non trivial, consiste dès lors à calculer cette charge de surface ; la partie la plus difficile étant de résoudre l'équation de Poisson avec une telle condition de manière analytique simple.

      

      n(r) est le vecteur normal de la surface en un point r et E^- (r) est le champ électrique total à l'intérieur de la surface en ce point. Les charges d'écran s devant se calculer de manière itérative (elles viennent s'ajouter aux cycles SCF de la molécule isolée), les méthodes incluant les effets de solvatation requièrent donc des temps de calculs plus longs.

      L'approche la plus simple utilise des séries de Taylor pour représenter l'expansion classique multipolaire de la structure électronique. Cette expansion est tronquée au terme dipolaire et seules les interactions des charges atomiques et des dipôles avec le milieu sont donc prises en compte. L'approche SCRF utilise une cavité idéale (sphérique ou ellipsoïdale) qui permet une solution analytique pour le calcul de l'énergie d'interaction entre le multipôle du soluté et celui du continuum. Ces simplifications conduisent à des problèmes de précision, et cette méthode est très sensible au choix du rayon de la cavité, mais pas tant à la constante diélectrique (pour les solvants particulièrement polaires).

      Ce modèle est implémenté en standard dans les programmes comme « GAMESS » ou le « GAUSSIAN » de la manière la plus simple possible :

• utilisation d'une cavité sphérique
• le potentiel électrostatique du soluté est représenté par sa charge (dans le cas d'un ion) ou par le moment dipolaire

      L'interaction électrostatique du soluté ne peut être résumée en ces deux termes uniquement. Au final, la restriction de la cavité sphérique n'est donc pas représentative de la véritable forme du solvant, et seul dans les cas spéciaux de molécules particulièrement sphériques, le modèle SCRF peut se montrer suffisant.

      Récemment, une approche de type continuum utilisant une généralisation du formalisme de Born pour l'interaction entre les charges atomiques partielles et le milieu diélectrique a été proposée [52]. Dans le principe, les monopoles centrés sur les atomes génèrent tous les multipôles requis pour représenter la distribution électronique.

      Une méthode plus sophistiquée encore, dénommée « Polarizable Continuum Model » (PCM) a été développée par Tomasi et ses collaborateurs [45-47]; celle-ci permet de travailler avec des cavités de forme plus réaliste, avec une surface découpée en une sorte de mosaïque constituée de petits polygones sphériques. L'interaction électrostatique entre le soluté et le solvant est dans ce cas décrit par un ensemble de charges ponctuelles polarisables, placées au centre de chaque petit 'morceau' (tessera). Ce modèle est donc beaucoup plus versatile en termes de description réaliste de la cavité et plus précis en ce qui concerne l'énergie due à l'interaction électrique entre le soluté et le milieu environnant.

      La méthode PCM place ainsi le soluté dans une cavité formée par l'union de sphères centrées sur chaque atome et le potentiel électrostatique du soluté est décrit par la production d'une charge apparente (de surface) sur la surface de la cavité, ce qui implique un plus grand réalisme pour l'interaction électrostatique. Le traitement par ordinateur divise la surface en de petits morceaux sur lesquels la charge (et sa contribution au gradient) est évaluée. Sur la base de différentes études, on a défini la taille de ces sphères comme ayant un volume équivalent à environ 1,2 fois le rayon de Van der Waals [45-50].

      Le modèle COSMO-PCM (CPCM) représente quant à lui une approche différente basée sur l'implémentation du « Conductor like Screening Model (COSMO) of solvation » [49-50]. Dans le modèle COSMO, le milieu environnant est décrit par un conducteur et non plus par un milieu diélectrique (e = Ľ), permettant de fixer les conditions limites initiales. Les termes d'énergie calculés en premier lieu pour le conducteur, sont ensuite divisés par un facteur de scaling décrit par la fonction :

      

      où x est un facteur de correction empirique (fixé par comparaison avec les valeurs obtenues pour des cas analytiques simples impliquant un milieu diélectrique) et e est la constante diélectrique (ici de l'eau), ce qui permet de revenir au milieu diélectrique originel.

      Cette technique simplifie les calculs d'interactions électrostatiques et les corrections sont effectuées à posteriori pour le comportement diélectrique. Les implémentations actuelles de ce modèle incluent le calcul de multipoles allant jusqu'aux hexadecapoles pour représenter la densité de charge de la molécule de soluté. Cette distribution induit à son tour une distribution de charge à la surface de la cavité et cela est pris en compte dans les cycles de calculs SCF, ce qui permet un traitement auto-cohérent pour les fonctions d'ondes moléculaires et les charges de la surface.

      Il est généralement reconnu que les erreurs de cavité sont plus faibles dans la méthode COSMO-PCM (CPCM) que dans la méthode PCM seule, ceci étant dû à l'utilisation, dans COSMO, de conditions limites exprimées en termes de potentiel électrostatique plutôt qu'en termes de champ électrique.

      Ces modèles ont cependant de nombreuses limitations ; l'une des plus importantes étant qu'ils ne permettent pas de tenir compte de l'aspect dynamique des effets entre le soluté et le solvant (liaisons hydrogène, par exemple). Malgré cela, ces méthodes de solvatation peuvent être utilisées (approche du continuum ; méthodes SCRF et PCM) afin d'améliorer les énergies et les géométries des espèces chimiques intervenant dans mécanismes réactionnels, par exemple.

3.2.1 Adsorption du catéchol

      Par spectroscopie infra-rouge il est possible d'observer la modification des fréquences de vibration des deux molécules lorsqu'elles sont adsorbées (le catéchol et le méthanol perdent l'un des hydrogènes des groupes -OH lors de l'adsorption). Porchet et collaborateurs ont observé que les deux bandes n_st -OH du catéchol à 3663 et 3603 cm^-1 (correspondant aux deux isomères détectables de cette molécule) disparaissent lors de son adsorption sur la surface de g-alumine [1-3].

      

Fig. 3.2 : Comparaison des fréquences de vibration du catéchol libre (spectres du haut) et adsorbé (spectres du bas).

      Les vibrations du cycle aromatique ne sont quant à elles pas modifiées et les auteurs en ont conclu que le catéchol ne se place pas parallèlement au plan de la surface (comme dans le cas d'une adsorption p) ; le plan de la molécule fait en réalité un angle de 118-120° avec la surface, comme il l'a été observé par Taylor et collaborateurs [31]. Ceci explique la sélectivité vis-à-vis de la méthylation en position C3 (la plus accessible).

      

Fig. 3.3 : Représentation schématique du catéchol adsorbé.

      Dans cette configuration, la molécule transfère un proton à la surface de g-alumine et l'ion phénoxyde en résultant est chimiquement adsorbé sur la surface. Le second groupe -OH est fixé à la surface via une liaison hydrogène [3]. La sélectivité découlant de l'angle de 120° peut donc être expliquée par des considérations stériques : le méthanol réagit depuis la surface où il est lui aussi adsorbé [29-31] et la distance entre l'oxygène du catéchol (site de l'alkylation dans le cas de la formation du guaiacol) et la surface d'alumine est très courte, ce qui favorise la formation du guaiacol (2-méthoxy-phénol). L'autre site d'alkylation conduisant au 3-méthyl-catéchol est lui aussi très proche, ce qui explique l'ordre de sélectivité guaiacol > 3-méthyl-catéchol.

      Le modèle de surface proposé par Knözinger et Ratnasamy [35], basé sur des études effectuées par Peri [32-33] sur des surfaces d'alumine a permis de mettre en évidence le fait que celle-ci contient différentes sortes de groupes hydroxyles. La fréquence de vibration -OH la plus élevée (à 3730 cm^-1) dans le spectre IR de la g-alumine correspond au groupe -OH le plus basique de la surface (entouré de quatre oxydes stabilisant l'ion aluminium insaturé). Le second hydroxyle le plus basique ne côtoye quant à lui que trois oxydes et se trouve à côté d'un aluminium portant une charge positive (bande à 3688 cm^-1).

      

Fig. 3.4 : Représentation schématique de la surface de g-alumine.

      Ces deux bandes disparaissent lorsque le catéchol est adsorbé sur la surface de g-alumine (ceci se voit facilement sur la figure III.2 : pic "négatif" à 3688-3730 cm^-1). Lorsque l'on chauffe le système à 500 °C en présence d'air, la bande à 3688 cm^-1 est restaurée, mais la bande à 3730 cm^-1 ne l'est pas. Les groupes hydroxyles de la surface peuvent cependant être régénérés en la chauffant en présence de vapeur d'eau. L'un des groupes -OH du catéchol perd son proton lors de l'adsorption et forme, avec le groupe -OH le plus basique de l'alumine, une molécule d'eau, ce qui explique pourquoi la désorption ne reconstitue pas la bande à 3730 cm^-1. Le deuxième hydroxyle le plus basique de la surface ne participe pas à la déprotonation (car il n'est pas suffisamment basique), mais il peut prendre part au phénomène d'adsorption par la formation d'une liaison hydrogène; la fréquence de vibration est alors décalée mais peut être restaurée après désorption du catéchol.

      Dans un article plus récent, Porchet et collaborateurs [3] ont proposé une hypothèse différente selon laquelle le catéchol perd ses deux protons pour s'adsorber sur deux ions aluminium de la surface. Les fréquences de vibration des liaisons C-O perturbées étant ainsi modifiées.

      Taylor et Lundlum [31], avaient déjà proposé deux modes différents pour l'adsorption du phénol sur une surface d'alumine: l'un où le phénol perd son proton et un autre où l'adsorption se fait via une liaison hydrogène. Le catéchol est un cas plus compliqué puisqu'il possède deux groupes -OH ; néanmoins, quel que soit le mode d'adsorption, la structure du catéchol ainsi adsorbé sur la surface est adéquate pour favoriser l'alkylation sur l'oxygène ou sur le carbone C3. D'autre part, les propriétés amphotères de la g-alumine sont très importantes ; les groupes -OH basiques catalysant l'adsorption des réactants et des produits sur les ions aluminium.

3.2.2 Adsorption du méthanol

      L'adsorption du méthanol est similaire à celle du catéchol: la liaison O-H est rompue, comme il l'a été confirmé par des études isotopiques [20]. Le spectre IR représenté par la figure III.5 montre bien l'absence de la bande à 3712 cm^-1 correspondant à la vibration stretching O-H.

      

Fig. 3.5 : Comparaison des fréquences de vibration du méthanol libre et adsorbé.

      Dans de nombreux travaux, il est accepté le fait que le méthanol forme une liaison covalente avec la surface de g-alumine (par départ d'une molécule d'eau), et les données des spectres infrarouges semblent confirmer cette hypothèse [29-36].

      L'adsorption des alcools sur les oxydes est une réaction du type acide-base et il est établi que ceux-ci se comportent de manière analogue à l'eau. D'après les informations fournies par Porchet [1-3], les espèces résultant de cette adsorption sont principalement des méthoxyles bidentés liés à deux acides de Lewis (les Al³⁺ de la surface du catalyseur). Les groupes hydroxyles isolés de la surface sont alors perturbés et les groupes les plus basiques peuvent déprotoner l'alcool. La chimisorption sur un site acide polarise la liaison C-O et il en résulte l'apparition d'une charge partielle positive sur le groupe méthyle, ce qui augmente son caractère électrophile, comme il a été proposé par Moravek [21].

      

Fig. 3.6 : Mode d'adsorption réversible des alcools proposé par Moravek [21].

      La région de 4000-3100 cm^-1, caractéristique des vibrations d'élongation des groupes -OH, montre la disparition, après l'adsorption sur la surface du catalyseur, de la bande entre 3712 et 3660 cm^-1 (pic central à 3680 cm^-1); l'adsorption provoque également la disparition des vibrations des groupes hydroxyles de la g-alumine entre 3780 et 3650 cm^-1 (bande principale à 3730 cm^-1). La région des fréquences O-H de la surface stabilisée par des liaisons hydrogène (entre 3650 et 3300 cm^-1) est, de plus, faiblement perturbée.

      Après l'adsorption, la bande large des vibrations d'élongation du groupe -CH₃ du méthanol gazeux est transformée en deux bandes bien définies (à 2949 et à 2844 cm^-1) caractéristiques de la présence des groupes méthoxyles adsorbés à la surface du catalyseur. La bande obtenue expérimentalement à 2949 cm^-1 correspond à la vibration d'élongation asymétrique du -CH₃ et la bande à 2844 cm^-1 correspond quant à elle à la vibration symétrique. Ce second pic possède une « épaule » à 2824 cm^-1; ce phénomène a été observé par Busca et collaborateurs [20] sur la d-alumine après adsorption du méthanol à température ambiante. Selon ces auteurs, il s'agit de deux espèces de surface qui se distinguent par la coordination de l'ion aluminium auquel l'oxygène du méthanol est lié.

      La vibration de déformation angulaire de la liaison O-H du méthanol (à 1330 cm^-1) disparaît après l'adsorption. Sur la g-alumine on n'observe pas de bandes caractéristiques du méthanol physisorbé (déformation angulaire du groupe -OH à 1480, 1440 ou 1420 cm^-1 suivant la coordination des ions aluminiums).

      La liaison C-O du méthanol gazeux est caractérisée par une bande d'adsorption située à 1034 cm^-1. Si le méthanol était physisorbé à la surface du catalyseur, il devrait montrer une fréquence de vibration C-O faiblement perturbée. L'adsorption dissociative des alcools sur des surfaces d'oxydes montre cependant un déplacement de la fréquence de stretching C-O vers des nombres d'onde plus élevés ; la liaison semble donc se renforcer et prendre un caractère de double liaison [31]. Lorsque le méthanol est adsorbé sur la g-alumine, on observe une bande principale à environ 1090 cm^-1, ainsi qu'une petite épaule à 1186 cm^-1. Cette bande correspond à la vibration d'élongation de la liaison C-O des groupes méthoxyles de surface, alors que l'apparition de la bande à 1186 cm^-1 est associée avec la déformation dans le plan du groupe -CH₃ du méthanol adsorbé à la surface.

      Les bandes d'adsorption correspondant à des nombres d'onde supérieurs à 1110 cm^-1 sont généralement associées à des espèces méthoxyles monodentées, c'est à dire liées à un seul cation métallique. Les vibrations qui absorbent à des fréquences inférieures à 1100 cm^-1 sont, quant à elles, spécifiques d'espèces polydentées. D'après les résultats obtenus par Porchet [3], l'adsorption du méthanol conduit à la formation d'espèces polydentées principalement. La réactivité de ces différentes espèces est différente, mais une réaction nécessitant la formation d'un ion électrophile CH₃⁺ sera plus aisée avec une espèce bidentée puisque la liaison C-O est dans ce cas plus polarisée [31].

3.4.1 Les techniques de modélisation possibles

      Plusieurs modèles de surface et de modes d'adsorption ont été étudiés afin d'obtenir des résultats les plus proches possible de l'expérience. L'approche du cluster d'atomes a été utilisée à cet effet.

      Différentes études ont montré que la surface de g-alumine peut être modélisée par de petits clusters d'atomes ne contenant que 1-3 atomes d'aluminium [17-19]. La condition étant que chaque atome d'aluminium doit être saturé de groupes -OH ou HOH [19]. De plus, pour un modèle de surface (110) comme celui considéré dans ce travail, le cluster doit contenir des atomes d'aluminium présentant les deux types de coordination (tétraédrique et octaédrique).

      L'avantage de l'utilisation du modèle du cluster d'atomes pour simuler une surface entière réside dans la taille relativement petite du système à calculer, ce qui ne nécessite pas des temps de calculs trop longs. Cependant, les clusters utilisés sont trop petits pour prétendre reproduire correctement le comportement d'une surface quasi infinie. Pacchioni [69,70] a montré que cette méthode donne tout de même d'assez bons résultats pour l'étude de la chemisorption, pour le calcul des fréquences de vibration ou encore des spectres de photoémission (pour un système CO adsorbé sur MgO, par exemple), et l'introduction de charges ponctuelles permet en outre d'ajouter les effets dus au potentiel de Madelung provenant de l'environnement autour du cluster. Ce potentiel, qui tient compte des phénomènes électrostatiques uniquement, permet de mieux décrire l'adsorption d'une molécule sur la surface, mais il ne permet toutefois pas de tenir compte de la contribution orbitalaire entre la molécule s'adsorbant et les atomes substrats de la surface.

      Ainsi, afin d'étudier le phénomène d'adsorption, différents clusters de surface de la g-alumine ont donc été considérés afin de simuler la surface entière en y liant de manière covalente un ion méthoxyle (résultant de l'adsorption d'une molécule de méthanol sur la surface), en comparant à chaque fois les fréquences de vibration calculées avec l'expérience. Puis l'un de ces clusters a été entouré de charges ponctuelles (embeded cluster model) afin de simuler l'effet des autres atomes de la surface et de reproduire le potentiel de Madelung généré par celle-ci.

3.4.2 Construction du modèle de la surface de g-Al₂O₃

      Le modèle de g-alumine a été construit à l'aide de l'interface Crystal builder du programme « CERIUS² » [26] à partir des données cristallographiques connues [27].

      La g-alumine possède trois types d'aluminium (avec des taux d'occupation cristallographique différents), mais seuls deux d'entre eux ont été considérés, le taux d'occupation du troisième aluminium étant très faible [32-36]. Grâce aux coordonnées cristallographiques, il a été possible de générer un cristal de g-alumine.

---

---

3.4.3 Adsorption du méthanol - Modèles de clusters simples

      Idéalement, l'étude de l'adsorption devrait se faire en utilisant le plus grand cluster possible pour modéliser la surface, mais ceci n'est pas réalisable à cause des temps de calculs prohibitifs que cela entraînerait. Après examen de la surface, on voit que celle-ci n'est pas régulière à cause des atomes d'aluminium non équivalents (tétraédriques et octaédriques); comme il l'a été déjà suggéré, le site d'adsorption le plus vraisemblable pour le méthanol devrait être l'un de ceux-ci. Plusieurs clusters différents ont été considérés et leurs caractéristiques sont résumées ci-après.

      

Fig. 3.13 : Représentations des différents cluster étudiés et de leurs caractéristiques. Les liaisons entre les atomes d'aluminium et d'oxygène ne sont que fictives puisqu'il s'agit d'une surface; celles-ci servent à rendre la représentation des clusters un peu plus claire.

      Ces différents clusters ont été découpés dans la surface de manière à contenir au moins un aluminium octaédrique et un aluminium tétraédrique ; pour assurer la neutralité, les aluminiums ont été saturés par des groupes hydroxyles et par des groupes -OH₂⁺ pour contrebalancer l'excès de charges négatives. Il faut remarquer que d'autres sites sont possibles si l'on clive le cristal selon des plans ayant des indices différents que (110), mais ceux-ci n'ont pas été considérés pour des raisons déjà évoquées.

      Le cluster II, de formule brute [Al₃O₉H₁₀]⁺, contenant un aluminium tétraédrique et deux aluminiums octaédriques (la présence du second aluminium octaédrique étant nécessaire pour décrire le site d'adsorption correctement) a conduit aux résultats les plus proches de l'expérience, comme il va l'être présenté ci-après.

      

Fig. 3.14 : Représentations du cluster d'atomes (cluster II) avec le méthoxyle coordonné ; la formule brute du système est [Al₃O₉CH₃O]^10-H₁₀. Les sept hydrogènes H_s permettent de saturer les liaisons O-Al et les hydrogènes H_n ont été ajoutés afin de rendre le système neutre.

      Le modèle d'adsorption décrit par le système ci-dessus a conduit à des résultats très proches de l'expérience et donne ainsi crédibilité à celui proposé par Moravek et collaborateurs [21], dans lequel le méthoxyle est lié de manière covalente à un aluminium tétraédrique et forme une interaction stabilisante avec l'aluminium octaédrique proche :

      

Fig. 3.15 : Mode d'adsorption réversible des alcools proposé par Moravek [21].

      Il n'a malheureusement pas été possible de comparer les géométries calculées avec l'expérience, puisqu'il n'existe pas de données structurales de l'adsorbat sur la surface d'alumine [1]. Si l'on compare les tables III.1 et III.3, on peut cependant remarquer que la liaison C-O devient plus courte avec l'adsorption (1,412 Å contre 1,418 Å pour B3LYP) ce qui est en accord avec Berteau et collaborateurs [22] qui avaient conclu que la liaison C-O prend un caractère de double liaison lors de l'adsorption. De plus, l'angle Al-O-C dans l'adsorbat est plus grand que l'angle C-O-H dans le méthanol libre et différents effets peuvent en être à l'origine ; parmi ceux-ci, la formation d'une liaison hydrogène avec un groupe -OH de surface proche ou des effets dus à la surface de g-alumine.

      

Fig. 3.16 : Représentations du système complet de formule brute [Al3O9CH3O]10-H10.

      

Tabl. 3.3 : Géométries du méthanol à l'état adsorbé. Les distances sont en Å et les angles en degrés.
Paramètres	HF	B3LYP	BP86
	6-31G**	6-31G**	Bases III
d (Al-O)	1.783	1.795	1.796
d (C-O)	1.394	1.412	1.427
< ; (Al-O-C)	116.7	116.00	110.38
< ; (O-C-H1)	111.03	111.63	110.05
< ; (O-C-H2)	110.39	110.60	110.77
< ; (O-C-H3)	111.53	110.18	109.26
< ; (Al-O-C-H3)	180.00	180.00	180.00

      

Tabl. 3.4 : Fréquences de vibration (en cm-1) calculées pour l'adsorbat.
Mode vibrationnel	HF	B3LYP	BP86	Expérience b
	6-31G**	6-31G**	Bases III
n C-O	1096	1078	1079	1090
d H-C-O	1174	1148	1122	---
d H-C-H	1131	1183	1159	1186
d CH3	1412	1457	1368	---
d H-C-H	1459	1463	1421	---
d H-C-H	1453	1506	1426	---
ns C-H	2840	2872	2912	2824
na C-H	2890	2962	2976	2844
na C-H	2868	3000	3042	2949
a Le facteur de scaling adéquat a déjà été appliqué.b Référence [2].

      Les vibrations ont été comparées, lorsque cela a été possible, avec celles fournies par Porchet [1-3], et celles-ci sont assez proches des fréquences obtenues expérimentalement (voir table III.4).

      Les résultats du calcul des fréquences HF/6-31G** sont très proches de l'expérience puisque la fréquence de la liaison C-O ne diffère que de 6 cm^-1 pour le mode de stretching, par exemple. Les fréquences obtenues montrent, de plus, qu'il n'y a aucune bande caractéristique d'espèces physisorbées (absence de bandes de type bending à 1480, 1440 et 1420 cm^-1 pour le méthanol).

      Si le méthanol était physisorbé, il devrait en effet être caractérisé par un mode stretching C-O à 1034 cm^-1 analogue à celui de la molécule libre en phase gazeuse. Or, aucune bande n'a été obtenue pour cette fréquence. La liaison C-O est au contraire caractérisée par un mode stretching à 1090 cm^-1, ce qui montre que durant l'adsorption dissociative du méthanol un déplacement des fréquences stretching vers des valeurs plus élevées a lieu. Ainsi, la liaison C-O devient plus forte et montre effectivement un caractère de double liaison [31] (table III.5).

      

Tabl. 3.5 : Déplacements des fréquences de vibration (en cm-1) entre le méthanol libre en phase gazeuse et le méthanol adsorbé calculés à l'aide de différentes méthodes (les fréquences en grisé des tables 3.2 et 3.4 ont été considérées).
Ecarts des fréquences	HF a	B3LYP a	BP86 a	Expérimentaux b
	6-31G**	6-31G**	Bases III
Dn (C-O)	67	47	60	57
Dn (H-C-O)	195	161	155	148
a (Dn = nadsorbé-nlibre)b Référence [2].

3.4.4 Modèle du cluster enrobé par des charges ponctuelles

      Des charges ponctuelles ont été introduites dans le but de simuler les effets électrostatiques dus à la surface de g-alumine et essayer ainsi d'améliorer les fréquences de vibration obtenues par le calcul. Ces effets peuvent en effet être reproduits en remplaçant les atomes d'aluminium et d'oxygène de la surface immédiatement voisins du cluster d'atomes découpé par des charges ponctuelles.

      Cette méthode a cependant posé beaucoup de problèmes à l'époque de cette étude car l'optimisation de la géométrie ainsi que le calcul des fréquences de vibration avec des charges ponctuelles n'est pas possible avec le GAUSSIAN 94. Les fréquences de vibration ont pour cette raison dû être calculées « manuellement ».

      Pour ce faire, les vecteurs de déplacement atomiques donnés par le GAUSSIAN (dans le cas du système cluster-méthoxyle sans charges ponctuelles) ont été utilisés pour évaluer les fréquences dans le cas du système cluster-méthoxyle enrobé de charges ponctuelles. La géométrie est alors variée pas à pas selon le mode normal considéré, et l'énergie est calculée à chaque pas (calcul single point). Les fréquences sont ensuite déterminées à partir de la courbe d'énergie potentielle qui en résulte et cette procédure est répétée pour chacun des modes normaux de vibration. Cette méthode a l'avantage de conduire à l'obtention de toutes les fréquences de vibration étant donné qu'elle permet d'étudier tous les modes normaux ; il est néanmoins très important que le centre de masse ne varie pas lorsqu'on ajoute les charges ponctuelles.

      Cette technique a initialement été appliquée à deux clusters sans l'ajout de charges ponctuelles (clusters II et V), afin de tester la validité de la méthode, et pour permettre une comparaison entre les fréquences obtenues sans les charges ponctuelles et avec les charges ponctuelles (voir les résultats présentés en annexe).

      Pour obtenir les vecteurs de déplacement des atomes du méthoxyle en évitant toute erreur due au fait que certains modes vibrationnels impliquent aussi des atomes de la surface, il a fallu effectuer un calcul des fréquences de vibration du méthoxyle seul (non lié au cluster), à la géométrie optimisée pour le système complet méthoxyle-cluster, afin de pouvoir ensuite utiliser les vecteurs de déplacements obtenus pour le calcul des single points (en attribuant un déplacement nul aux atomes du cluster). Cette méthode a conduit à des résultats satisfaisants puisque le centre de masse du système entier est conservé (celui de la surface ne se déplace pas puisque celle-ci est fixe, alors que pour le méthoxyle, le déplacement selon les coordonnées normales maintient le centre de masse fixe par définition). Les résultats correspondants sont résumés en annexe.

      Pour l'étude des fréquences de vibration du méthoxyle adsorbé avec l'ajout des charges ponctuelles, un nouveau cluster d'atomes totalement symétrique a été découpé de la surface de g-alumine précédemment modélisée, et l'ensemble des charges ponctuelles a été choisi, lui aussi, de manière à être totalement symétrique (d'où le choix d'un cluster, le cluster V, possédant un plan symétrie vertical, plutôt que le cluster II, moins symétrique) afin que le méthoxyle ressente un champ électrostatique le plus homogène possible, avec une charge de -1 distribuée sur 1003 atomes. Chaque atome enrobant le cluster a donc été remplacé par une charge correspondant à son état d'oxydation (+3 pour les atomes d'aluminium et -2 pour les atomes d'oxygène), car d'après la littérature ceci constitue une bonne approximation pour les surfaces ayant un caractère ionique assez prononcé [69-70].

      Les résultats obtenus pour le système, avec et sans les charges ponctuelles sont présentés dans la table 3.6.

      Etant donné que les charges ponctuelles influencent de manière assez importante la géométrie du méthoxyle ; il a fallu ré-optimiser les longueurs de liaison ainsi que les angles du méthoxyle par single points avant le calcul des fréquences (en variant la position des atomes selon les coordonnées normales). La liaison C-O s'allonge en particulier d'environ 10 % lorsque le méthoxyle se trouve en présence des charges ponctuelles ; cela s'explique par le champ électrique créé par les charges qui a un effet répulsif sur le méthyle (la charge de l'aluminium étant plus grande que celle de l'oxygène).

      

Fig. 3.17 : Images du système méthoxyle-cluster (représentation en space filling) et du reste de la surface l'entourant (représentée en bâtonnets). Ces atomes ont été remplacés par des charges ponctuelles.

      

Tabl. 3.6 : Fréquences de vibration (en cm-1) obtenues pour le cluster V avec et sans les charges ponctuelles.
Type de vibration	Sans charges	Avec charges	Expérience	Différence
n -C-O	1012	700 ª	1090	-390
d H-C-H	1120	1030	1186	-156
d H-C-O	1153	---	---	---
d -CH3	1432	---	---	---
d H-C-H	1471	1402	---	---
d H-C-H	1495	---	---	---
nst -CH	2860	2813	2824	-11
nst -CH	2928	2888	2844	44
nst -CH	2968	2918	2949	-31
a Après ré-optimisation de la liaison C-O.

      Le calcul des fréquences de vibration a montré que celles-ci sont généralement plus basses avec l'ajout des charges ponctuelles, ce qui signifie que les effets de charges ont pour conséquence l'affaiblissement des liaisons.

      La table 3.6 montre que mis à part pour le stretching C-O, l'introduction des charges ponctuelles semble améliorer les fréquences des autres modes stretching, alors que les modes bending sont nettement moins bons. Ceci provient vraisemblablement du fait que la géométrie n'est que grossièrement optimisée pour le système enrobé de charges ponctuelles ; les modes bending ressentent les effets dus au champ électrique de manière plus importante que les stretching.

3.5.1 Influence du choix du cluster

      Le modèle du cluster d'atomes a conduit à des résultats proches de l'expérience ; l'erreur commise sur les fréquences de vibration oscille en effet entre 10 et 60 cm^-1. Le mode d'adsorption du méthanol a pu ainsi être rationalisé et comparé à celui proposé par Moravek [21].

      Cette étude a de plus mis en évidence l'importance des groupes -OH de la surface. Ces groupes, en permettant la formation de liaisons hydrogène avec le méthyle, stabilisent en effet le système et rendent l'adsorption encore plus favorable. L'utilisation d'un cluster plus gros n'a, par contre, pas permis d'améliorer la qualité des fréquences de vibration calculées, mais ceci est certainement dû aux dimensions modestes de la molécule de méthanol.

3.5.2 Problèmes posés par les charges ponctuelles

      L'introduction des charges ponctuelles a posé un très grand nombre de problèmes étant donné l'impossibilité d'effectuer des optimisations de géométrie ou des calculs de fréquences sur de tels systèmes par la version 94 du « GAUSSIAN » utilisée pour ce travail. Ainsi, beaucoup de temps et d'énergie ont été dépensés afin de trouver une méthode qui puisse contourner ce problème. La technique « manuelle » pour le calcul des fréquences de vibration s'est démontrée être assez fiable et simple à utiliser, à condition de pouvoir effectuer un calcul préliminaire qui fournisse les vecteurs de déplacements correspondants aux modes normaux ; pour des systèmes plus gros tels que le catéchol, cela nécessiterait cependant des temps de calculs plus longs. D'autres méthodes, comme par exemple les techniques semi-empiriques (beaucoup plus rapides) pourraient être envisagées dans ce cas (soit pour le calcul des fréquences, soit pour l'obtention des vecteurs de déplacement).

      L'ajout des charges ponctuelles n'a pas semblé apporter grand chose à la problématique ; un cluster de taille plus grande contenant plusieurs couches d'atomes aurait peut-être dû être utilisé afin de réduire les effets électrostatiques trop importants sur le méthoxyle qui y est lié ; effets provoqués par les charges ponctuelles ajoutées (surtout pour les liaisons proches de la surface comme la liaison C-O).

4.1.1 La théorie du champ cristallin et la théorie du champ des ligands

      La théorie du champ cristallin (Crystal Field Theory) permet de rationaliser les interactions entre un métal et ses différents ligands, et fournit ainsi une voie très utile pour la compréhension des spectres électroniques ainsi que des propriétés thermodynamiques de ce type de composés. Les bases de ce modèle ont été proposées par Bethe et Van Vleck qui ont étudié l'effet d'un potentiel électrostatique créé par la présence de ligands sur les niveaux d'énergie d'un ion libre se trouvant dans une maille cristalline. Cette théorie consiste à placer n charges ponctuelles aux positions occupées par les ligands, et à étudier les effets résultant des interactions électrostatiques entre ces charges et les électrons d du métal. Dans le cas d'un complexe de symétrie octaédrique ML₆ ces auteurs ont ainsi montré que les orbitales d du métal, dégénérées dans le cas de l'ion libre, sont toutes déstabilisées par la présence des ligands et une levée partielle de leur dégénérescence a lieu (figure 4.1).

      

Fig. 4.1 : Levée de la dégénérescence des orbitales atomiques pour un métal dans une symétrie Oh.
Ion libre	Champ moyen (sphérique) de L6	Champ octaédrique de L6

      Ainsi, les orbitales d ayant leur lobes orbitalaires entre les ligands (d_xy, d_xz et d_yz) voient leur énergie diminuer légèrement (orbitales t_2g), alors que les orbitales se trouvant orientées selon l'axe des ligands (d_x²_-y², d_z²) sont sujettes à une forte répulsion électrostatique due aux ligands, et voient leur énergie augmenter (orbitales e_g). Celles-ci sont déstabilisées car l'une des orbitales ressent l'influence des ligands axiaux (d_z²) et l'autre ressent la répulsion des quatre ligands équatoriaux (d_x²_-y²). Les orbitales d_xy, d_xz et d_yz du métal sont quant à elles stabilisées par rapport au champ moyen, car elles ressentent moins la répulsion du champ des ligands dans le complexe.

      Ce modèle électrostatique ne reproduit naturellement pas de manière réaliste les interactions covalentes basées sur une approche orbitalaire, et le modèle plus réaliste du champ des ligands est en général utilisé. Dans ce modèle, les orbitales du métal se combinent avec celles des ligands de symétrie identique, et dans le cas d'un complexe de symétrie octaédrique (avec des ligands n'ayant pas d'orbitales p ou p*), les orbitales d_xy, d_xz et d_yz du métal restent de nature métallique (set t_2g) et seules les d_z² et d_x²_-y² (set e_g) vont se combiner avec les orbitales provenant des différents ligands à cause de leur symétrie. Les orbitales e_g se combineront donc avec celles des ligands en formant respectivement deux orbitales liantes et deux orbitales anti-liantes.

      On aura, par exemple, pour un complexe de symétrie octaédrique basé sur des interactions de type s uniquement, un diagramme d'orbitales moléculaires analogue à celui indiqué dans la figure 4.2. Si l'on considère que 12 électrons proviennent des ligands et occupent les orbitales de basse énergie a_1g, t_1u et e_g, les électrons d provenant du métal occuperont les orbitales t_2g et e_g*. Cela amène à la notion d'éclatement octaédrique D_oct (e_g*-t_2g) introduit par la théorie du champ cristallin qui permet de rationaliser la stabilité des complexes. Ainsi, on trouvera par exemple fréquemment des métaux d⁶ avec une configuration « bas spin » dans les complexes à 18 électrons, comme indiqué à la figure 4.3.

      

Fig. 4.2 : Représentation de la combinaison des orbitales atomiques du métal et des ligands [48].

      Les systèmes d⁶ bas spin à 18 électrons sont remarquablement stables car les six ligands amènent formellement 12 électrons et le métal n'amenant que 6 électrons, seules les orbitales t_2g liantes seront remplies, laissant ainsi les orbitales e_g* vides.

      

Fig. 4.3 : Configuration électronique dans un système t_2g⁶ à spin bas.

      Il existe cependant de nombreuses exceptions, comme par exemple le système Fe(OH₂)₆²⁺, dans lequel le fer est dans la configuration « haut spin ». L'énergie d'appariement des électrons requise dans ce cas est en effet plus grande que celle provenant de l'éclatement octaédrique. Il s'agit donc de faire un compromis entre l'énergie d'appariement et l'énergie provenant de l'éclatement octaédrique.

      La différence d'énergie entre les orbitales e_g et les orbitales e_g* dépend naturellement du caractère s-donneur des ligands dans le complexe, et la stabilité de celui-ci dépendra donc de tous ces divers paramètres (spin bas/spin haut, nature des ligands, etc).

      

Fig. 4.4 : Importance des interactions métal-ligand et effet sur les orbitales du complexe.
Interactions M-L faibles conduisant à une faible stabilisation des eg et une faible déstabilisation des eg*	Interactions M-L fortes conduisant à une forte stabilisation des eg et une forte déstabilisation des eg*

      Il faut encore noter que bien que le rôle des orbitales p des ligands soit très important pour la stabilisation de certains systèmes par effet de p-retrodonation, ce phénomène n'est pas possible dans le cas des complexes hexa-aquo étudiés dans le cadre de ce travail car il n'existe pas d'orbitales ou d vacantes dans ces systèmes ; les orbitales t_2g du métal restent donc quasiment de nature métallique et sont non-liantes dans ce type de complexe.

4.1.2 Complexes inertes et complexes labiles

      L'une des réactions fondamentales dans la chimie de coordination est le remplacement de l'un des ligands du métal par un autre ligand ; cette réaction est appelée « réaction de substitution ». Ces réactions procèdent selon une palette de vitesses très étendue ; le temps de réaction peut en effet aller de quelques nanosecondes, pour les aqua-ions de cuivre(II), à plus de 300 ans pour les aqua-ions d'iridium(III) ; la constante de vitesse s'étalant sur plus de 18 ordres de grandeurs.

      

Fig. 4.5 : La figure montre le temps de résidence d'une molécule d'eau dans la première sphère de coordination d'un ion métallique donné, ainsi que la constante de vitesse de l'échange correspondant, k_ex = 1 / _ex (illustration tirée de la référence [76]).

      Il est en général admis de séparer les complexes en deux catégories : les complexes labiles et les complexes inertes. Cette description empirique est basée sur le temps employé par la réaction de substitution pour se faire. Taube a proposé un modèle pour ces réactions dans lesquelles un ligand coordonné au métal central est remplacé par un autre ligand [61] :

      

      Si le processus est complété en moins d'une minute (à 298 K avec une concentration de réactifs valant 0,1 M), le complexe sera considéré comme étant labile ; si la réaction prend plus de temps, le complexe sera alors dit inerte [49,61]. Cette propriété est naturellement liée au type d'ion et à son état d'oxydation.

      Il est maintenant bien établi que les complexes de chrome(III) [61], de cobalt(III) [107], de rhodium(III) [8-9,59,106] et d'iridium(III) [10] sont particulièrement inertes [93]. On constate que cela concerne les complexes de métaux d³ ou de métaux d⁶ à spin bas. Orgel [94], puis Jørgensen [95] avaient déjà mis en évidence, au milieu du siècle dernier, le fait que la stabilisation due au champ des ligands est déterminante pour la cinétique d'une réaction de substitution ou d'échange.

      Basolo et Pearson [50] ont utilisé une approche basée sur le champ des ligands afin d'essayer de rationaliser ces observations. En se basant sur les travaux de Hush [93], ces auteurs ont montré comment il est possible d'associer l'énergie liée à l'effet de stabilisation due au champ des ligands (LSFE) à l'inertie d'un complexe d'un métal dⁿ donné, ainsi qu'à son mode de réaction de substitution (ceci en termes de D_oct). En comparant l'énergie LSFE associée au complexe octaédrique de départ à l'énergie associée aux états de transition impliqués dans les deux mécanismes d'échange envisageables, il est possible de déterminer quel mécanisme sera préférentiellement suivi.

      Les deux mécanismes d'échange possibles sont le mécanisme limite associatif, dans lequel le métal a un nombre de coordination plus élevé à l'état de transition (mécanisme analogue à la réaction S_N2 organique), et le mécanisme limite dissociatif, dans lequel le métal passe par un nombre de coordination plus bas (mécanisme analogue à la substitution S_N1 organique). Le mécanisme limite associatif implique donc un état de transition hepta-coordonné alors que le mécanisme limite dissociatif implique un état de transition penta-coordonné. L'espèce penta-coordonnée peut exister avec une symétrie pyramidale à base carrée ou trigonale bipyramidale, alors que l'espèce hepta-coordonnée sera de symétrie pentagonale bipyramidale.

      Il est donc possible d'évaluer l'énergie due à la stabilisation du champ des ligands en faisant comme approximation que la magnitude du champ des ligands ne varie globalement pas lors du changement de coordination (variation du nombre de ligands), ceci se justifiant par le fait que la perte d'un ligand est compensée par la modification des distances de liaisons des ligands restant. La variation de l'énergie de stabilisation due à l'effet du champ des ligands entre le complexe de départ et l'état de transition est appelée « énergie d'activation du champ des ligands » (LFAE). Une diminution de cette énergie de stabilisation (LFAE > 0 selon la définition proposée) amènera donc une contribution positive à l'énergie d'activation globale requise par le processus (augmentation), alors qu'une contribution négative produira une diminution de l'énergie d'activation requise. L'énergie d'activation due au champ des ligands n'est toutefois qu'une composante de l'énergie d'activation totale ; il faut encore tenir compte en effet des énergies de rupture et de formation des liaisons des groupes entrant et sortant.

      Les résultats collectés par ces auteurs ont pu cependant montrer que l'énergie requise pour les complexes d³ et d⁶ à spin bas est positive, quelque soit le type de coordination ou la géométrie de l'état de transition [50].

      

Fig. 4.6 : La contribution de l'énergie de stabilisation des ligands pour un ion d3 octaédrique vaut - 1,2Doct. Les énergies estimées pour l'état de transition penta-coordonné et pour l'état de transition hepta-coordonné valent respectivement - 1,0Doct et -0,774Doct, et conduisent à des « énergies d'activation » dues au champ des ligands de + 0,2Doct (penta-) et + 0,426Doct (hepta-).
Octaèdre	Pyramide à base carrée (penta-coordonnée)	Bipyramide pentagonale (hepta-coordonnée)

      D'après l'exemple présenté dans la figure 4.6, on pourrait penser que le mécanisme impliquant un état de transition penta-coordonné sera favorisé pour les systèmes d³ car l'énergie d'activation requise est plus faible que pour le mécanisme passant par un état de transition hepta-coordonné. Les études successives sur les mécanismes d'échange ont cependant montré que cette conclusion est fausse [1,3-4,51-54]. Les calculs simplifiés des énergies d'activation dues au champ des ligands ne permettent donc pas une prédiction du mécanisme suivi ; il faudrait pour cela utiliser un meilleur modèle de l'état de transition et tenir compte des effets de la seconde sphère de coordination.

      Ces calculs ont cependant l'intérêt de montrer que l'énergie d'activation due au champ des ligands est une contribution importante à l'enthalpie libre d'activation de Gibbs DG^‡_exp, c'est-à-dire à la réactivité des ions des métaux de transition.

4.1.3 Mécanismes de substitution et d'échange de solvant : définitions

      Les réactions d'échange de solvant et plus particulièrement de molécules d'eau sur les aqua-ions des métaux sont fondamentales pour la compréhension de la réactivité de ces métaux dans les systèmes biologiques et chimiques. La compréhension de la réactivité intrinsèque de ces aqua-ions est en effet importante puisque le remplacement d'une molécule d'eau de la première sphère d'hydratation est une étape clé dans les réactions de formation de complexes. Les observations faites pour le Ni²⁺ ont montré que la connaissance des mécanismes d'échange de solvant est nécessaire pour la compréhension des mécanismes de substitution en général [1].

      Dans une telle réaction d'échange, les réactants et les produits sont identiques ; les profils d'énergie sont donc caractérisés par l'absence d'une force thermodynamique poussant la réaction à se faire puisque la variation d'enthalpie libre de réaction de Gibbs vaut zéro.

      

      En 1965 déjà, Langford et Gray [56] proposèrent un système de classification pour les réactions de substitution selon le type de mécanisme : celles-ci peuvent être de type associatif (A) dans lesquelles un intermédiaire ayant un degré de coordination plus élevé est détecté, dissociatif (D), dans lesquelles un intermédiaire de coordination plus basse est détecté, et de type concerté (I), dans lesquelles aucun intermédiaire n'est trouvé. Les chemins réactionnels A et D procèdent donc en deux étapes et font intervenir des intermédiaires respectivement hepta- et penta-coordonnés ; le mécanisme concerté n'impliquant quant à lui qu'une seule étape.

      Langford et Gray proposèrent, d'autre part, de distinguer les mécanismes réactionnels caractérisés par un mode d'activation associatif (a) dans lesquels la constante de vitesse est plus sensible aux variations du groupe entrant que du groupe sortant, et ceux caractérisés par un mode d'activation dissociatif (d) où la constante de vitesse est influencée par le groupe sortant plus qu'elle ne l'est par le groupe entrant. Naturellement, tout mécanisme D doit être dissociativement activé, de même que tout mécanisme A doit être associativement activé. Les mécanismes concertés I sont caractérisés par un large spectre d'états de transition dans lesquels le degré de formation de liaison entre le ligand entrant et le métal central varie de l'important (mécanismes I_a) au négligeable (mécanismes I_d) [51,53].

      Une réaction d'échange de solvant doit naturellement être symétrique ; ainsi, pour un mécanisme I_d avec un groupe entrant possédant une faible tendance à la formation de liaison, le groupe sortant devra lui aussi être faiblement lié au métal. Inversement, pour un mécanisme I_a, les ligands entrant et sortant devront tout deux être caractérisés par une liaison plus forte et plus courte avec le métal (ceci est présenté dans les figures 4.7 et 4.9).

      L'approche habituelle pour l'élucidation des mécanismes de substitution implique l'étude de la dépendance de la vitesse de réaction avec la concentration des réactants, le pH, la force ionique, ainsi que la nature du solvant. Dans les réactions d'échange de solvant ces critères ne sont pas applicables, et il faut donc utiliser les paramètres d'activation obtenus par des études à température et pression variables : les mécanismes sont alors attribués en se basant sur les paramètres thermodynamiques comme l'enthalpie d'activation DH^‡, l'entropie d'activation DS^‡, l'enthalpie libre d'activation DG^‡ ou encore le volume d'activation DV^‡ [1-2].

      Dans ce contexte, l'avantage principal du volume d'activation DV^‡ est qu'il est facilement compréhensible en termes de mouvements atomiques uniquement, l'interprétation du DS^‡ impliquant des facteurs moins tangibles et plus difficiles à interpréter. La variation de volume est en effet quelque chose de directement perceptible par les sens humains, alors que l'entropie est quelque chose de beaucoup plus abstrait. Ainsi, il est plus facile d'élaborer des théories basées sur le DV^‡ plutôt que sur le DS^‡, comme suggéré par Swaddle [39].

      Merbach et ses collaborateurs ont donc proposé d'utiliser systématiquement le volume d'activation DV^‡ comme critère d'identification du mécanisme [51]. Celui-ci permet en théorie d'attribuer un mécanisme à une réaction de substitution en général, et à une réaction d'échange de solvant en particulier. Le volume d'activation est défini comme étant la différence de volume molaire partiel entre les espèces à l'état de transition et les réactants de départ. Il est considéré comme étant la somme de deux contributions ; une contribution intrinsèque DV^‡_intr due aux changements de conformation du complexe lors du passage des réactifs à l'état de transition (variations dans les distances intra-atomiques durant la formation de l'état de transition) et une contribution d'électrostriction DV^‡_elec due aux changements de moments dipolaires et de charges du solvant :

      DV^‡_exp = DV^‡_intr + DV^‡_elec

      Dans le cas des réactions d'échange de solvant et pour des ligands neutres, la contribution d'électrostriction peut être considérée comme nulle ou négligeable. Le volume d'activation mesuré sera alors déterminé par la composante intrinsèque DV^‡_exp » DV^‡_intr, et il sera donc directement lié aux transformations prennant place dans la première sphère de coordination.

      Sur cette base, la valeur du volume d'activation, DV^‡, peut être positive ou négative. De ce fait, le mécanisme attribué sera D ou A respectivement. Entre ces deux mécanismes limites se trouvent les mécanismes concertés I, pour lesquels la valeur de DV^‡ est proche de zéro ; ceux-ci peuvent être caractérisés par des modes d'activation (d) ou (a), selon que l'influence du ligand partant est plus grande que celle du ligand entrant, ou l'inverse (mécanismes I_d ou I_a pour lesquels les valeurs du volume d'activation sont petites et positives ou petites et négatives) [1-2].

      

      

Fig. 4.7 : Effets de la pression sur la constante de vitesse k en fonction du signe du volume d'activation DV^‡ : pour un mécanisme (d) activé, une augmentation de la pression provoquera une diminution de la vitesse de réaction, alors que pour un mécanisme (a) activé l'effet inverse sera observé [102].

      Dans le cas des mécanismes limites, D et A, le volume d'activation ne peut pas excéder ±V⁰, c'est-à-dire le volume molaire partiel du solvant. En fait, cette valeur limite doit être nettement inférieure pour tenir compte de la contraction ou de l'expansion des liaisons avec les molécules de solvant qui ne s'échangent pas.

      D'un point de vue structurel, la seule différence entre les mécanismes I_d et I_a est le degré d'expansion de l'état de transition. Arbitrairement, on parlera d'un mécanisme I lorsque DV^‡ est voisin ou égal à zéro.

      

Fig. 4.8 : Variations du volume en fonction du mécanisme de substitution suivi [102].

      Swaddle a proposé des valeurs de DV^‡ (reliées aux intermédiaires réactionnels) pour les deux mécanismes limites [110] ; le DV^‡ mesuré expérimentalement n'est cependant pas relié de manière simple au mécanisme, et d'autre part le volume molaire de l'état de transition (qui est la quantité mesurée par l'expérience) est plus petit que celui de l'intermédiaire pentacoordonné correspondant, ou plus grand que l'intermédiaire heptacoordonné [3,4], ce qui explique pourquoi les valeurs limites estimées par Swaddle sont rarement atteintes. En général, le DV^‡ ne permet donc de n'attribuer que le mode d'activation (a ou d) de la réaction de substitution, sauf dans le cas où le DV^‡ mesuré est très grand positif, ou très grand négatif [111]. C'est par exemple le cas du Ti(OH₂)₆²⁺ où le DV^‡ vaut -13,5 cm³/mol et est très proche de la valeur prédite par Swaddle pour le volume d'un intermédiaire heptacoordonné (attribution d'un mécanisme A).

      Sur cette base, d'après Rotzinger, il est important de garder en mémoire que dans la plupart des cas, les paramètres d'activation expérimentaux, en particulier le DV^‡, ne permettent pas de distinguer des mécanismes A/D de mécanismes I_a/I_d. Ainsi, d'après cet auteur pas tous les mécanismes proposés dans la littérature sur la base de mesures expérimentales sont à considérer comme étant définitifs [111].

      Comme il l'a déjà été dit, le volume d'activation DV^‡ est défini comme étant la différence entre le volume molaire partiel de l'état de transition et celui du réactant à une température T. Il est expérimentalement possible de déterminer les paramètres (pseudo) thermodynamiques (comme le volume d'activation DV^‡) et cinétiques (constante de vitesse d'échange k_ex) par des techniques spectroscopiques (UV, MS, etc) ou par des techniques de RMN dynamique avec, pour les réactions plus lentes, couplage avec des méthodes de marquage isotopique. La loi cinétique décrivant l'échange isotopique peut être exprimée sous la forme :

      

      où k est la constante de vitesse, x est la fraction molaire de ligand coordonné et x_Ľ est la fraction molaire de ligand coordonné à l'équilibre. Par intégration de l'équation (1), il est possible d'obtenir la relation entre la fraction molaire x et la constante de vitesse k :

      

      L'expression (2) permet de décrire la diminution de x en fonction du temps, et celle-ci est déterminée par l'étude de la décroissance du signal RMN correspondant au ligand lié (ou du signal du ligand libre, selon le type de marquage) et par ajustement des valeurs expérimentales obtenues à l'équation (2).

      Selon la théorie du complexe activé, la constante de vitesse de réaction k_ex, peut être reliée aux paramètres d'activation par la relation d'Eyring :

      

      où k = transmission probability coeeficient (k » 1)

      et k_B = constante de Boltzmann

      En mettant cette équation sous la forme logarithmique, on exprime l'enthalpie libre d'activation en fonction de T et de k_ex :

      

      En dérivant le terme de l'enthalpie libre en fonction de la pression à température constante, on obtient alors le volume d'activation DV^‡ qui permet d'exprimer la dépendance de la constante de vitesse k en fonction de P :

      

      La constante de vitesse d'échange k_ex observée expérimentalement peut soit être diminuée, soit être augmentée par une variation de la pression, ceci dépendant du signe du volume d'activation. La dépendance de la constante de vitesse k_ex, avec la pression P, peut donc être reliée au volume d'activation au moyen de l'équation suivante :

      

      ce qui permet d'en tirer la valeur du DV^‡ et de caractériser ainsi le mécanisme d'échange.

      La dépendance de la constante de vitesse avec la température permettra, de plus, d'en tirer les autres paramètres thermodynamiques tels que le DH^‡ et le DS^‡ par ajustements à l'aide de l'équation (3) où l'on a remplacé l'expression de DG^‡ :

      

4.1.4 Mécanismes de substitution et d'échange des aqua-ions di- et tri-valents de la première série des métaux de transition : quelques résultats expérimentaux

      Comme il l'a déjà été dit, les réactions d'échanges d'eau peuvent s'écrire de la manière suivante :

      

      Il a été expérimentalement observé ces dernières années que les ions divalents et trivalents de la première série des métaux de transition présentent un changement progressif dans le mécanisme de substitution [58]. Ainsi, les métaux de transition de la partie gauche du tableau périodique substituent plutôt selon un mécanisme A ou I_a, alors que les métaux de transition de la partie droite substituent avec un mécanisme I_d voire D. Le changement du mode d'activation est observé après la configuration électronique d⁵ et, d'autre part, le long d'une colonne du tableau périodique, il y a passage vers des mécanismes de nature de plus en plus associative.

      Pour la première période des métaux de transition, Merbach et ses collaborateurs ont obtenu la valeur du volume d'activation DV^‡ la plus négative pour l'échange d'eau sur le Ti(III) [54] et la plus positive pour le Ni(II) [55], comme le montrent les valeurs résumées dans les tables 4.1. Les valeurs de DV^‡ plus proches de zéro obtenues expérimentalement pour les autres éléments di- et trivalents de la première série des métaux de transition ont conduit à l'attribution de mécanismes I avec passage continu d'un mode (a) à un mode (d).

      

Tabl. 4.1a : Valeurs du volume d'activation DV‡  en fonction de la configuration électronique pour l'échange d'eau autour d'ions di- et trivalents [1,11,52,102].
M(OH2)63+	Ti3+	V3+	Cr3+	Fe3+	Ga3+
dn	d1	d2	d3	d5	d10
DV‡ cm3/mol	-12.1	-8.9	-9.6	-5.4	+5.0
Mécanisme	A, Ia	Ia	Ia	Ia	Id

      

Tabl. 4.1b. Valeurs du volume d'activation DV‡  en fonction de la configuration électronique pour l'échange d'eau autour d'ions di- et trivalents [1,11,52,102].
M(OH2)62+	V2+	Mn2+	Fe2+	Co2+	Ni2+
dn	d3	d5	d6	d7	d8
DV‡ cm3/mol	-4.1	-5.4	+3.8	+6.1	+7.2
Mécanisme	Ia	Ia	Id	Id	Id

      Comme il l'a été dit, dans un complexe octaédrique, en absence de liaisons p, les orbitales t_2g sont non-liantes et les orbitales e_g* sont s* anti-liantes. Les tables ci-dessus indiquent que le remplissage des orbitales t_2g rend l'approche d'une septième molécule vers la face de l'octaèdre de moins en moins favorable électrostatiquement et permet d'expliquer la tendance vers des mécanismes de moins en moins associatifs. Le remplissage successif des orbitales e_g* facilite quant à lui la dissociation d'une molécule de ligand.

      Conclusion : lorsqu'on traverse une série des métaux de transition, on passe d'un mécanisme d'échange à caractère (a) à un mécanisme d'échange à caractère (d).

      Ainsi, par exemple le Cr³⁺ (t_2g³) échange des molécules d'eau selon un mécanisme I_a, alors que le Ga³⁺ (e_g⁴) suit plutôt un mécanisme I_d.

4.1.5 Etudes théoriques d'échange de solvant : l'approche de Rotzinger

      Etant donné que les intermédiaires réactionnels ont une durée de vie très courte, ils sont généralement inaccessibles par l'expérience. De plus, il n'est pas évident de distinguer un mécanisme limite A d'un mécanisme I_a, ou un mécanisme limite D d'un I_d, d'où l'importance et l'utilité des techniques de modélisation moléculaire à l'aide de l'ordinateur.

      Plusieurs études théoriques portant sur l'échange d'eau dans les ions hydratés des métaux de transition ont été effectuées ces dernières années. Åkesson et collaborateurs [33] ont étudié, les premiers, à l'aide de méthodes quantiques, l'échange d'eau pour les métaux de transition de la première période.

      Ces travaux ont cependant fait l'objet de plusieurs critiques [3], car la méthode pour la détermination du mécanisme d'échange proposée par ces auteurs n'était pas très rigoureuse, et les résultats obtenus ont été interprétés de manière erronée à cause des états de transitions non optimisés qu'ils ont obtenus. Ils ont de plus proposé de se baser uniquement sur les énergies d'activation DE^‡ calculées entre états de transition et réactants afin de déterminer le mécanisme réactionnel préférentiellement suivi (le mécanisme calculé avec la plus faible énergie d'activation étant favorisé). Rotzinger a montré que pour le vanadium(II) étudié par Åkesson et collaborateurs, les deux mécanismes D et I_a ont des énergies d'activation identiques et ce critère n'est donc pas fiable pour décider du mécanisme qui est préféré. D'autre part, ces auteurs ont calculé des énergies d'activation sur la base d'espèces qui ne correspondaient pas à des états de transition, mais à des intermédiaires réactionnels. Pour le mécanisme dissociatif des cations trivalents des métaux étudiés par Åkesson, les énergies des états de transition et des intermédiaires sont très proches, ce qui permet d'expliquer pourquoi ils ont en général obtenu d'assez bons résultats pour ces cas.

      Dans son article de 1996, Rotzinger a proposé une méthode élégante pour l'étude théorique du mécanisme réactionnel de ces réactions d'échange, en obtenant une excellente corrélation avec l'expérience [3].

      D'après cette méthode, afin de déterminer le mécanisme d'échange suivi, les trois mécanismes possibles (A, D et I) doivent être étudiés afin de pouvoir comparer les paramètres d'activation calculés avec l'expérience.

      

      Les différentes espèces mises en évidence sur le chemin réactionnel calculé (réactants, états de transition et intermédiaires éventuels) sont à chaque fois caractérisées au moyen du calcul des fréquences de vibration (fréquences positives pour les réactants/produits et les intermédiaires ; une fréquence de vibration imaginaire pour les états de transition). Le chemin réactionnel le plus favorable étant alors identifié comme celui ayant la plus basse énergie d'activation, et l'attribution du mécanisme possible par comparaison avec les données expérimentales (énergie d'activation et volume d'activation expérimentaux) [3-4].

      DE_a^‡ = E(TS) - E(GS)

      correspondant à la réaction réactant ® état de transition.

      Rotzinger a montré que sept molécules d'eau (hexa-aqua ion avec ajout d'une molécule d'eau de la seconde sphère de coordination) sont nécessaires pour une étude correcte des mécanismes associatifs ou concertés (A, I_a ou I_d), mais que l'hexa-aqua ion seul, sans l'ajout de molécules d'eau additionnelles, suffit pour le mécanisme dissociatif [3,4]. La septième molécule d'eau peut naturellement être ajoutée pour l'étude d'un mécanisme D, mais son influence sur la structure de l'état de transition est négligeable.

      Le modèle proposé implique donc un réactant de départ composé du métal de transition et de six molécules d'eau, pour un mécanisme dissociatif D (équation 2), et un adduit à sept molécules d'eau pour un mécanisme associatif A (équation 3) ou concerté I (équation 4) :

      

      Lorsqu'un état de transition est obtenu par le calcul, il faut encore vérifier qu'il s'agit d'un véritable point de selle de premier ordre en calculant les deuxièmes dérivées de l'énergie (conduisant à une seule fréquence de vibration imaginaire). Puis, il faut contrôler que l'état de transition peut effectivement être relié aux réactifs et aux produits (à l'aide d'un calcul de type IRC, « Intrinsic Reaction Path », par exemple).

      

Fig. 4.9 : Représentation des différentes espèces impliquées dans les divers mécanismes possibles [111].

      D'après Rotzinger, en vertu du principe de la réversibilité microscopique, les états de transition dans lesquels les ligands entrant et sortant ne sont pas symétriques et équivalents doivent être suivis d'intermédiaires réactionnels dans lesquels ces groupes sont symétriques et équivalents. Pour qu'une réaction d'échange puisse avoir lieu il faut en effet une étape où les ligands entrant et sortant sont symétriquement équivalents (soit pour l'état de transition, soit pour l'intermédiaire) [3,4].

      Les variations des longueurs de liaison M-O, DSd(M-O) durant la phase d'activation indiquent si une compression ou une élongation se produit durant la réaction, et cette variation peut être corrélée à la composante intrinsèque du volume d'activation (DV^‡_int). On peut en effet montrer que l'élongation ou la compression d'une liaison donnée durant le processus d'activation affecte usuellement les autres liaisons « spectatrices » :

      

      Le problème est rendu compliqué car tous les paramètres thermodynamiques mesurés expérimentalement décrivent la somme d'effets provenant du solvant, de la seconde sphère de coordination et du métal de transition lui-même. Pour l'échange d'eau, la contribution au DV^‡ due à l'électrostriction de la seconde sphère de coordination et des molécules d'eau du solvant est néanmoins faible, et la valeur du volume d'activation expérimental reflète principalement les changements dans la première sphère de coordination. En raison du nombre d'approximations faites, la valeur absolue de DSd(M-O) calculée n'a toutefois pas de signification, et seul le signe de DSd(M-O) n'a de sens immédiat. Il permet néanmoins d'attribuer avec plus ou moins de certitude le type de mécanisme suivi, et pour les aqua-ions des métaux de transition il a été montré que le signe de DSd(M-O) correspond à celui du volume d'activation [3,4,32].

      Il est d'autre part possible de définir le degré de formation et le degré de rupture des liaisons à l'état de transition pour les mécanismes D et A (respectivement d_form et d_break) de la manière suivante :

      

Mécanisme D :
Mécanisme A :

      où :

• d_max est la longueur de liaison pour la limite dissociative ; celle-ci correspond à la distance M-O de la molécule d'eau qui se trouve dans la seconde sphère d'hydratation de l'espèce [M(OH₂)₆(OH₂)]ⁿ⁺
• d_normal est la longueur de liaison M-O « normale », définie comme étant la moyenne des six liaisons spectatrices dans [M(OH₂)₆(OH₂)]ⁿ⁺
• est la distance M O (active) à l'état de transition
• sont les longueurs de liaisons « normales » à l'état de transition

      Les valeurs ainsi calculées permettent de construire des diagrammes de type More-O' Ferral utiles pour la discussion des mécanismes. Les DV^‡_cal dépendront de trois facteurs : la magnitude de la liaison normale M-O, le degré de formation ou de rupture de liaison (exprimé par d_form ou d_break) et la distance M O à l'état de transition (d_A^TS ou d_D^TS).

      Ce modèle possède naturellement des limitations, puisque mis à part le fait que les molécules de solvant de la seconde sphère de coordination sont négligées, les effets du solvant et l'influence des contre-ions éventuels ne sont pas pris en compte non plus. Ainsi, l'attribution du mécanisme sur la base des calculs théoriques ne peut être faite de manière certaine que lorsque les changements de structures obtenus par le calcul (exprimés par les DSd[M-O]) se corrèlent aux résultats expérimentaux, de même que lorsque l'énergie d'activation calculée est proche de celle obtenue par l'expérience.

      Le paramètre DSd(M-O) décrit les modifications des longueurs de liaison intervenant dans le système pour atteindre l'état de transition et n'est donc qu'une représentation approchée du DV^‡. Il faut aussi remarquer que les énergies d'activation DE^‡ calculées à l'aide de simulations à l'ordinateur correspondent à des processus ayant lieu en phase gazeuse et à une température de 0 K, alors que le DG^‡ correspond à une réaction en solution et à 298 K. Les énergies du point zéro, les capacités calorifiques, les entropies d'activation, les phénomènes de solvatation ainsi que les énergies dues à la formation de liaisons hydrogène devraient donc être prises en compte dans une telle étude. Toutefois, ceci n'a que peu d'importance dans le cas qui nous intéresse, car seules de grandes différences d'énergies (états de transition / produits ou réactifs) sont calculées (le reste étant « petit »).

      Approximations mises à part, les calculs théoriques permettent d'obtenir les structures et les énergies des états de transition et des intermédiaires réactionnels impliqués dans les réactions d'échange ou de substitution ; chaque type de mécanisme procèdant naturellement par un état de transition caractéristique. Pour illustrer la méthode proposée par Rotzinger, nous allons reprendre les résultats obtenus par cet auteur pour les hexa-aqua ions de Ti(III), V(II) et Ni(II).

      

Fig. 4.10 : Etats de transition pour l'échange d'eau dans les aqua-ions de Ti(III), V(II) et Ni(II) [3,4].

      Comme le montrent les figures 4.10 et 4.11, dans le cas du titane(III), l'état de transition a une symétrie C₁ et sa fréquence de vibration imaginaire décrit un mouvement de rapprochement du ligand entrant vers le centre métallique. Le calcul du volume molaire partiel des réactants, des états de transition et des intermédiaires est difficile, mais la méthode basée sur le calcul de la différence des sommes de toutes les longueurs de liaison métal-ligands DSd(M-O) entre les états de transitions et le réactant initial a toujours montré une excellente corrélation avec l'expérience [3,4]. Les énergies de ces espèces ainsi que les DSd(M-O) correspondants sont indiquées dans la figure 4.11. Comme il l'a été décrit par Rotzinger, dans cette réaction d'échange, l'entrée du ligand domine sans aucun doute possible le processus d'activation, et le mécanisme peut donc être identifié comme étant de type A. L'intermédiaire [Ti(OH₂)₅ (OH₂)₂]³⁺ est quant à lui caractérisé par des fréquences positives et par une symétrie C₁. Le mécanisme devant obéir à la règle de la réversibilité microscopique, l'échange de ligand ne peut donc se faire que si à un moment donné le ligand entrant et le ligand sortant deviennent (symétriquement) équivalents, ainsi, un second état de transition symétrique suit l'intermédiaire sur le chemin réactionnel du titane(III), comme il est montré à la figure 4.11.

      En ce qui concerne l' aqua-ion vanadium(II), l'état de transition {[V(OH₂)₅ (OH₂)₂]²⁺}^‡ a une symétrie C₂ et indique, dans ce cas, un mécanisme de type concerté, comme le confirme l'absence d'intermédiaire réactionnel. Les ligands entrant et sortant sont en effet symétriquement équivalents et non discernables l'un de l'autre. La valeur négative de DSd(M-O) indique, d'autre part, que la formation de liaison à l'état de transition est plus importante que la rupture, ce qui est caractéristique d'un mécanisme concerté possédant un faible caractère (a).

      Pour l'échange d'eau sur l'aqua-ion Ni(II), seul un état de transition pour un mécanisme D a pu être calculé et caractérisé par Rotzinger [3,4]. Celui-ci a montré que l'espèce {[Ni(OH₂)₅ (OH₂) (OH₂)]²⁺}^‡ a une symétrie C_s dans laquelle les ligands entrant et sortant sont bien discernables l'un de l'autre ; la fréquence de vibration imaginaire montrant principalement un mouvement de départ du ligand sortant. L'intermédiaire réactionnel [Ni(OH₂)₅ (OH₂)₂]²⁺ a quant à lui une symétrie C_2v et est une espèce pentacoordonnée pyramidale à base carrée. Le DSd(M-O) calculé indique un mode D, mais selon Rotzinger, un modèle plus précis pourrait toutefois transformer cet intermédiaire en l'état de transition d'un mécanisme I_d, la différence d'énergie entre les deux espèces étant très petite [3,4].

      

Fig. 4.11 : Profils des énergies et des distances de liaison pour les mécanismes A, I_a et D [3-4] des hexa-aqua ions de Ti(III), V(II) et Ni(II).

      Malgré les approximations faites, les résultats que Rotzinger a obtenus à l'aide de son modèle l'ont porté à faire les considérations suivantes : le mécanisme limite dissociatif D est théoriquement envisageable pour tout complexe de métaux de transition, mais il est par contre le seul possible pour les systèmes d⁶, d⁷, d⁸, d⁹ et d¹⁰ à spin haut à cause de la déstabilisation entraînée par l'occupation des orbitales antiliantes (e_g*) à l'état de transition [3,4] qui défavorise ainsi l'approche d'une septième molécule d'eau rendant tout mécanisme avec mode d'activation (a) impossible, et surtout favorise la dissociation d'un ligand.

      Les calculs ont pu montrer que le mécanisme associatif nécessite la condition que les métaux de transition n'aient pas plus de 7 électrons d (à cause de la nature des orbitales d à l'état de transition hepta-coordonné et de leur occupation) ; ainsi, d'après les calculs de Rotzinger, le Sc(III), le Ti(III) et le V(III) réagissent selon un mécanisme associatif A, alors que le Ni(II), le Cu(II) et le Zn(II) réagissent via un mécanisme dissociatif D ou concerté I_d [76,96]. Les éléments 3d du milieu du tableau périodique étant caractérisés par des mécanismes I_a/A et D (ou I_d).

      En conclusion, on peut donc dire qu'en l'absence de contraintes stériques imposées par des ligands de grande taille, le mécanisme suivi est déterminé principalement par le nombre d'électrons d du métal, et par le mode d'occupation des orbitales t_2g et e_g* dans le réactant initial [3-4].

4.2.1 Problème de l'interprétation mécanistique basée sur les données expérimentales et apport des méthodes de calculs

      Comme il l'a déjà été dit, les réactions d'échange d'eau sur les aqua-ions des métaux de transition di- et trivalents ont été le sujet de multiples études expérimentales [1-2]. Il a ainsi été constaté que pour les ions 3d octaédriques, le mécanisme d'échange passe progressivement d'un mode d'activation I_a à I_d avec l'augmentation du nombre d'électrons d et la diminution du rayon ionique.

      Ce changement est montré de la manière la plus évidente par le changement de signe du volume d'activation DV^‡, et a été confirmé par les études théoriques effectuées par Rotzinger aux niveaux Hartree-Fock et CAS-SCF [3-4]. Comme il l'a été dit, le changement progressif du mécanisme réactionnel ne peut être expliqué uniquement en terme de taille cationique car la configuration électronique joue aussi un rôle important. Pour les complexes octaédriques s, les orbitales t_2g sont de nature non-liantes, alors que les orbitales e_g* sont anti-liantes. Le remplissage graduel des orbitales t_2g situées entre les ligands va défavoriser électrostatiquement l'approche d'une septième molécule vers la face ou l'arrête de l'octaèdre et ainsi diminuer la facilité de former une liaison avec une nouvelle molécule de ligand entrant. De manière similaire, l'augmentation de l'occupation des orbitales e_g* pointant vers les ligands va augmenter la tendance à la rupture de liaison, favorisant ainsi les mécanismes D. Les effets électroniques permettent donc d'expliquer cette modification du mode d'activation.

      En se basant sur ces arguments, il est alors possible de prédire un mode d'activation dissociatif pour l'échange de molécules d'eau dans les aqua-ions octaédriques (t_2g⁶) à spin bas comme le Ru(OH₂)₆²⁺, le Rh(OH₂)₆³⁺ ou encore le Ir(OH₂)₆³⁺. Dans une première étude du mécanisme de substitution de ligands sur le Ru(OH₂)₆²⁺ il avait été montré que les constantes de vitesse pour la réaction de substitution d'une molécule d'eau par les anions Cl^-, Br^- et I^- étaient très similaires [5], indiquant ainsi des chemins réactionnels pour atteindre l'état de transition extrêmement proche (c'est à dire la partie concernant la dissociation d'une molécule d'eau). Plus tard, cette étude a été étendue à une large variété de ligands possédant des charges ainsi que des nucléophilicités différentes, et il a été clairement montré que la vitesse de formation du monocomplexe était indépendante de la nature du ligand entrant. Il a alors été attribué au Ru(OH₂)₆²⁺ un mécanisme I_d [6]. Une étude à pression variable de l'échange d'eau sur cet aqua-ion ayant cependant conduit à l'obtention d'un volume d'activation proche de zéro (DV^‡ = -0,4 cm³/mol), il a donc été interprété comme étant un mécanisme concerté I sans caractère (a) ou (d) prédominant [7].

      Le cas des hexa-aqua ions de rhodium(III) et d'iridium(III) est plus intriguant. Par la méthode de dilution isotopique par ¹⁸O (isotope ratio mass spectometer), un mécanisme D avait été attribué pour l'échange d'eau dans le complexe hexa-aquo de rhodium(III) par Plumb et Harris [8] ; la comparaison des constantes de vitesse pour la substitution d'une molécule d'eau par un anion Cl^- ou Br^- ayant validé ces observations par le même Harris [80]. Cependant, il y a quelques années, Merbach et collaborateurs ont obtenu, par des techniques de RMN haute pression sur l'oxygène ¹⁷O, un volume d'activation négatif pour l'échange d'eau sur le Rh(OH₂)₆³⁺ (DV^‡ = -4,2 cm³/mol) [9], et un volume plus négatif encore pour l'aqua-ion iridium(III), Ir(OH₂)₆³⁺ (DV^‡ = -5,7 cm³/mol) [10]. Ils en ont alors conclu que dans les deux cas un mécanisme concerté à faible caractère (a), a lieu.

      Ces deux attributions mécanistiques ont été remises en question par Richens. Il a été suggéré que dans le cas du Ru(OH₂)₆²⁺ le volume d'activation proche de zéro peut être dû à une contraction des liaisons des cinq ligands spectateurs pour atteindre l'état de transition dans un processus I_d [11-12]. Poursuivant ce raisonnement, Richens a proposé que dans le cas du rhodium(III), la charge posit4e plus élevée du métal pouvait produire une grande contraction de volume dans l'état de transition, suffisante pour changer le signe du volume d'activation et le rendre ainsi négatif [12], et cet effet devrait être encore plus marqué pour l'iridium(III). Selon cet auteur, l'interprétation du mécanisme selon un mode I_a aurait alors été fausse, un mécanisme limite D étant en fait à l'oeuvre (avec un DV^‡ expérimental mesuré négatif).

      En supposant qu'une telle hypothèse était vraie, ces deux cas montreraient les limites de l'utilisation du volume d'activation comme critère diagnostique du mécanisme d'échange suivi.

      Le but de ce travail de recherche, mené en collaboration avec F. Rotzinger et A. Merbach, était donc de résoudre cette énigme en étudiant théoriquement les mécanismes d'échange d'eau sur les hexaaqua ions de rhodium(III) et d'iridium(III) à l'aide du modèle développé avec succès par le même Rotzinger.

      Comme il va l'être vu, les résultats présentés ci-après et l'étude successive de Richens et de ses collaborateurs [100] sur la substitution d'anions Br^- sur l'aqua-ion Rh(OH₂)₆³⁺ a entre-temps permis de confirmer les conclusions de Merbach et de ses collaborateurs, et le même Richens a revu son hypothèse au sujet du volume d'activation.

4.3.1 Méthodologie

      Selon la méthode proposée par Rotzinger [3,4] pour élucider le mécanisme d'échange suivi, il faut étudier les différents mécanismes possibles (A, D ou I) à l'aide de structures de départ hexa-coordonnées ; une molécule d'eau additionnelle de la seconde sphère de coordination devant être ajoutée, selon le mécanisme que l'on souhaite étudier. Après avoir obtenu et caractérisé les différentes espèces chimiques sur les chemins réactionnels, les variations des distances DSd(M-O) sont analysées et les énergies d'activation sont alors comparées afin de déterminer le mécanisme préféré.

      Afin de localiser l'état de transition d'un mécanisme réactionnel donné, Rotzinger conseille de partir d'un réactant hexa-aquo [M(OH₂)₆]ⁿ⁺ ou de l'« adduit » [M(OH₂)₆OH₂]ⁿ⁺ (ayant toutes les fréquences de vibration réelles) et de sélectionner dans le complexe une liaison M-O qui va être variée (allongement ou compression) afin de simuler le mécanisme réactionnel, en optimisant à chaque variation les liaisons restantes. La structure de départ ne doit pas avoir une symétrie trop élevée (C₁ ou C_s), et les optimisations de géométrie sont effectuées avec cette contrainte sur l'une des liaisons, jusqu'à ce que les gradients soient < 0,005 hartree/bohr. La structure remplissant cette condition est alors soumise à un calcul des fréquences de vibration afin de déterminer s'il s'agit bien d'un état de transition (une seule fréquence imaginaire), puis optimisée en tant qu'état de transition.

      Pour l'étude de mécanismes de type associatif ou concerté, Rotzinger propose d'utiliser des adduits à sept molécules d'eau pour les réactifs (et les produits). Dans le cas d'un mécanisme limite A, l'état de transition est caractérisé par l'approche du ligand entrant plus que par le départ du ligand sortant, alors que dans le cas d'un mécanisme concerté les deux phénomènes seront équivalents (les mécanismes I_d/I_a différant cependant par le degré de formation des liaisons). Les mécanismes concertés seront, d'autre part, caractérisés par l'absence de tout intermédiaire réactionnel, contrairement aux mécanismes A ou D.

      Les espèces caractérisant les chemins réactionnels d'un mécanisme A et d'un mécanisme I seront :

      

      Dans un mécanisme limite dissociatif D, le réactant sera simplement le complexe octaédrique, et le mécanisme passera par un état de transition où le métal sera penta-coordonné. Rotzinger a montré que dans le cas d'un tel mécanisme l'influence de la molécule d'eau se trouvant dans la seconde sphère d'hydratation peut être négligée. En effet, l'ajout de cette molécule ne modifie pas le mécanisme D en un mécanisme I_d, et celle-ci peut donc être omise lors des calculs (les états de transition sont identiques avec et sans la septième molécule d'eau supplémentaire, en particulier pour les longueurs de liaison du groupe partant). Pour un mécanisme de type D on aura alors :

      

      L'état de transition pour ce mécanisme sera caractérisé par une fréquence de vibration imaginaire montrant l'une des six liaisons M-L s'allongeant (les cinq autres restant approximativement inchangées), ce qui correspond au mouvement de départ du ligand partant.

      Comme il l'a déjà été dit, dans le cas d'un mécanisme dissociatif, la septième molécule d'eau ajoutée ne modifie quasiment pas les six liaisons M-O restantes, mais par contre la présence de cette molécule supplémentaire pour les études des mécanismes A ou I est fondamentale (à cause de la possibilité de former des liaisons hydrogène).

      Il faut noter que les mécanismes de type « concerté », I, sont parfois compliqués à décrire puisqu'ils occupent une position intermédiaire entre le mécanisme limite associatif et le mécanisme limite dissociatif. Il est en outre souvent difficile de distinguer un mécanisme limite D d'un mécanisme I_d, surtout si la différence d'énergie entre l'état de transition et l'intermédiaire est faible. Dans le cas du Ni(OH₂)₆²⁺OH₂, par exemple, Rotzinger a montré que la fréquence imaginaire de l'état de transition correspondait à l'élongation de la liaison entre le métal et le groupe partant ; la distance avec la molécule se trouvant dans la seconde sphère de coordination ne variant pratiquement pas (état de transition dominé par le départ du ligand) [3-4]. Il en a donc déduit que le mécanisme calculé était de type D, voire I_d ; les limitations du modèle ne permettant pas une distinction plus précise.

---

4.3.2 Cas du rhodium(III)

---

---

---

---

4.3.3 Cas de l'iridium(III)

      Dans le cas du complexe hexa-aquo de l'iridium(III), le niveau de calcul Hartree-Fock n'est, à priori, pas suffisant pour l'étude des mécanismes d'échange, ceci à cause de la présence d'effets relativistes et de la corrélation électronique plus forte pour les métaux de transition des périodes profondes. Il a donc été tenté, dans un premier temps, d'utiliser les techniques DFT du programme « GAUSSIAN » (version 98). Malgré les nombreuses bases et fonctionnelles testées, les tentatives n'ont cependant pas permis d'obtenir un état de transition ou un intermédiaire réactionnel, et seuls les réactants de départ ont pu être identifiés (aqua-ion Ir(OH₂)₆³⁺ et adduit Ir(OH₂)₆(OH₂)³⁺).

      Les mêmes modèles et niveaux de calcul que ceux utilisés pour l'étude de l'aqua-ion rhodium(III) ont alors été repris (bases identiques et niveau de calcul Hartree-Fock), pour les raisons précédemment expliquées [3,4]. Ceci a amené à l'obtention de deux chemins réactionnels similaires à ceux obtenus dans le cas du rhodium(III), et l'identification successive des espèces les caractérisant a conduit à des résultats satisfaisants ; ceux-ci sont présentés ci-après.

      

Tabl. 4.9a : Energies et distances Ir-O pour les différentes espèces du mécanisme D à six molécules d'eau
Espèces	Symétrie	Energie, au	d(M-O), Å
[Ir(OH2)6]3+	D2h (réactant)	-559.0742	2.089; 2.089; 2.089; 2.089; 2.089; 2.089
{[Ir(OH2)5(OH2)]3+}‡	Cs (TS)	-559.0185	2.101 ; 2.040 ; 2.028 ; 2.074 ; 2.074 ; 3.498
[Ir(OH2)5(OH2)]3+	Cs (interméd.)	-559.0197	2.106 ; 2.037 ; 2.027 ; 2.074 ; 2.074 ; 3.986
L'ordre de numérotation des atomes est celui indiqué dans la figure IV.25.

      D'où on en tire finalement les différences d'énergie suivantes pour le mécanisme D :

      DE^‡ (Etat de transition-Réactant) = 146,14 kJ/mol

      DE (Etat de transition-Intermédiaire) = - 3,06 kJ/mol

      

Tabl. 4.9b : Variation des distances Ir-O et volumes calculés pour les différentes espèces du mécanisme D à six molécules d'eau
Espèces	S [d(M-O)], Å	Connolly a, Å3	Connolly b, Å3	Connolly c, Å3
[Ir(OH2)6]3+, GS	12.5334	153.24	165.17	159.18
{[Ir(OH2)5(OH2)]3+}‡, TS	13.8152	161.70	171.93	168.19
[Ir(OH2)5·(OH2)]3+, Interm.	14.3048	163.23	174.30	170.71
Estimation du DV‡	+1.282 Å d	+5.10 cm3/mol e	+4.07 cm3/mol e	+5.43 cm3/mol e
a Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.52 Å pour O et 1.2 Å pour H, 100 points / Å. b Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.88 Å pour O et 1.23 Å pour H, 100 points / Å c Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayon de Van der Waals de 1.90 Å pour O, H négligés, 100 points / Å d DS[d(M-O)] = S[d(M-O)] {Etat de transition} - S[d(M-O)] {Réactant} eDV‡ calculés après conversion des Å3/molécule en cm3/mol

      D'après les tables IV.9, on constate que le signe de DSd(Ir-O) est positif pour le mécanisme à six molécules d'eau, contrairement au signe du DV^‡ expérimental. La différence d'énergie entre l'intermédiaire réactionnel et l'état de transition est d'autre part très faible (état de transition et intermédiaire semblant se confondre), et ceci suggère que le mécanisme pourrait à nouveau être de type concerté, comme c'est le cas pour le rhodium(III), ce qui a successivement été étudié (tables IV.10).

      

Tabl. 4.10a : Energies et distances Ir-O pour les différentes espèces du mécanisme I à sept molécules d'eau
Espèces	Symétrie	Energie, au	d(M-O), Å
[Ir(OH2)6·(OH2)]3+	D2h (Réactant)	-635.1432	2.104; 2.072; 2.092; 2.088; 2.088; 2.076; 3.830
{[Ir(OH2)5(OH2)2]3+}‡	Cs (TS)	-635.0880	2.076; 2.076; 2.049; 2.085; 2.085; 2.737; 2.737
L'ordre de numérotation des atomes est celui indiqué dans la figure IV.25.

      

Tabl. 4.10b : Variation des distances Ir-O et volumes calculés pour les différentes espèces du mécanisme I à sept molécules d'eau
Espèces	S [d(M-O)], Å	Connolly a, Å3	Connolly b, Å3	Connolly c, Å3
[Ir(OH2)6]3+	16.35	173.51	182.43	179.09
{[Ir(OH2)5(OH2)2]3+}‡	15.85	170.14	178.30	172.20
Estimation du DV‡	-0.50 Å d	-2.03 cm3/mol e	-2.49 cm3/mol e	-4.15 cm3/mol e
a Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.52 Å pour O et 1.2 Å pour H, 100 points / Å. b Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.88 Å pour O et 1.23 Å pour H, 100 points / Å c Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayon de Van der Waals de 1.90 Å pour O, H négligés, 100 points / Å d DS[d(M-O)] = S[d(M-O)] {Etat de transition} - S[d(M-O)] {Réactant} e DV‡ calculés après conversion des Å3/molécule en cm3/mol

      On en tire finalement pour le mécanisme I :

      DE^‡ (Etat de transition-Réactant) = 144,59 kJ/mol

      Les résultats montrent que le mécanisme à sept molécules d'eau est énergétiquement favorisé par rapport au mécanisme D à six molécules d'eau (144,6 kJ/mol contre 146,1 kJ/mol). D'autre part, l'absence d'intermédiaires réactionnels, le signe négatif, ainsi que la valeur très faible de DSd(Ir-O) indiquent un mécanisme de type I, voire I_a, et confirment les résultats expérimentaux obtenus par Merbach et collaborateurs [10].

      Les effets de solvant ont ensuite été ajoutés à l'aide du modèle de Onsager (SCRF) ainsi que des modèles PCM/CPCM afin de valider ces observations, et les résultats en sont résumés ci-après.

      

Tabl. 4.11a : Energies et distances Ir-O (SCRF) pour les différentes espèces du mécanisme D à six molécules d'eau
Espèces	Symétrie	Energie, au	d(M-O), Å
[Ir(OH2)6]3+	D2h (réactant)	-559.5304	2.089; 2.089; 2.089; 2.089; 2.089; 2.089
{[Ir(OH2)5(OH2)]3+}‡	Cs (TS)	-559.4327	2.100 ; 2.042 ; 2.027 ; 2.074 ; 2.074 ; 3.493
[Ir(OH2)5·(OH2)]3+	Cs (interméd.)	-559.4101	2.105 ; 2.039 ; 2.027 ; 2.074 ; 2.074 ; 4.019
L'ordre de numérotation des atomes est celui indiqué dans la figure IV.25.

      

Tabl. 4.11b : Variation des distances Ir-O et volumes calculés (SCRF) pour les différentes espèces du mécanisme D à six molécules d'eau
Espèces	S [d(M-O)], Å	Connolly b, Å3	Connolly c, Å3
[Ir(OH2)6]3+	12.53	165.17	159.18
{[Ir(OH2)5(OH2)]3+}‡	13.81	171.96	168.33
[Ir(OH2)5·(OH2)]3+	14.34	175.72	171.04
Estimation du DV‡	+1.28 Å d	+4.09 cm3/mol e	+5.51 cm3/mol e
a Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.52 Å pour O et 1.2 Å pour H, 100 points / Å. b Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.88 Å pour O et 1.23 Å pour H, 100 points / Å c Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayon de Van der Waals de 1.90 Å pour O, H négligés, 100 points / Å d DS[d(M-O)] = S[d(M-O)] {Etat de transition} - S[d(M-O)] {Réactant} e DV‡ calculés après conversion des Å3/molécule en cm3/mol

      Ce qui nous donne ainsi :

      DE^‡ (Etat de transition-Réactant) = 256,43 kJ/mol kJ/mol

      DE (Etat de transition-Intermédiaire) = 59,09 kJ/mol kJ/mol

      On voit que l'effet stabilisant du solvant provoque une forte augmentation de DE^‡ pour le mécanisme D, de même que croit l'écart d'énergie entre l'intermédiaire et l'état de transition. On peut cependant constater que la valeur de DE^‡ obtenue par le calcul SCRF est anormalement grande (256 kJ/mol), de même que l'intermédiaire semble être moins stable que l'état de transition ! Ces artefacts proviennent de problèmes liés au modèle qui montre ses limites dans ce cas.

      

Tabl. 4.12a : Energies et distances Ir-O (SCRF) pour les différentes espèces du mécanisme I à sept molécules d'eau
Espèces	Symétrie	Energie, au	d(M-O), Å
[Ir(OH2)6]3+	D2h (GS)	-635.5437	2.104; 2.072; 2.092; 2.088; 2.088; 2.077; 3.832
{[Ir(OH2)5(OH2)2]3+}‡	Cs (TS)	-635.5293	2.076; 2.076; 2.049; 2.085; 2.085; 2.741; 2.741
L'ordre de numérotation des atomes est celui indiqué dans la figure IV.25.

      

Tabl. 4.12b : Variation des distances Ir-O et volumes calculés (SCRF) pour les différentes espèces du mécanisme I à sept molécules d'eau
Espèces	S [d(M-O)], Å	Connolly b, Å3	Connolly c, Å3
Ir(OH2)63+	16.35	182.43	178.56
{[Ir(OH2)5(OH2)2]3+}‡	15.85	178.56	172.73
Estimation du DV‡	-0.50 Å d	-2.33 cm3/mol e	-3.51 cm3/mol e
a Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.52 Å pour O et 1.2 Å pour H, 100 points / Å. b Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayons de Van der Waals de 1.88 Å pour O et 1.23 Å pour H, 100 points / Å c Surface de Connolly avec un rayon d'essai de 1.4 Å (molécule d'eau), rayon de Van der Waals de 1.90 Å pour O, H négligés, 100 points / Å d DS[d(M-O)] = S[d(M-O)] {Etat de transition} - S[d(M-O)] {Réactant} eDV‡ calculés après conversion des Å3/molécule en cm3/mol

      Ce qui nous donne alors pour le mécanisme I :

      DE^‡ (Etat de transition-Réactant) = 37,67 kJ/mol kJ/mol

      On peut une nouvelle fois remarquer que les énergies obtenues à l'aide du modèle SCRF pour ces espèces ne sont pas satisfaisantes. L'approximation sphérique de ce modèle n'est en effet suffisamment précise que pour des complexes de symétrie octaédrique (globalement comparable à une sphère), ce qui n'est pas le cas de l'état de transition ou de l'intermédiaire. Cela se constate facilement en observant la table IV.13 : de manière similaire aux espèces du rhodium(III), l'intermédiaire réactionnel semble être moins stable que l'état de transition, ce qui n'est pas possible !

      Enfin, comme l'indique la table IV.13, les énergies PCM/CPCM calculées à l'aide du programme « GAUSSIAN 98 » aux géométries SCRF ne semblent pas correctes pour le chemin à sept molécules d'eau. Ces même énergies ont donc été recalculées à l'aide du programme « GAMESS ». Il est à rappeler que seules les énergies ont été calculées à l'aide de ce modèle. Les résultats obtenus pour les deux mécanismes, à six et à sept molécules d'eau, sont récapitulés dans les tables ci-après.

      

Tabl. 4.13 : Energies obtenues pour les différentes espèces du mécanisme D à six molécules d'eau à l'aide de diverses techniques permettant d'inclure les effets de solvatation
	Réactant	Etat de transition	Intermédiaire	En. Activation
GAZ (GAMESS)	-559.0742	-559.0185	-559.0197	146.14
SCRF	-559.5304	-559.4327	-559.4101	(256.43)
PCM (G98)	-559.7894	-559.7380	-559.7414	134.81
CPCM (G98)	-559.7875	-559.7381	-559.7414	129.49
PCM (GAMESS)	-559.7256	-559.6645	-559.6661	160.06
CPCM (GAMESS)	-559.7299	-559.6738	-559.6746	147.11

      

Tabl. 4.14 : Energies obtenues pour les différentes espèces du mécanisme I à sept molécules d'eau à l'aide de diverses techniques permettant d'inclure les effets de solvatation
	Réactant	Etat de transition	En. Activation
GAZ (GAMESS)	-635.1432	-635.0880	144.59
SCRF	-635.5436	-635.5293	(37.67)
PCM (G98)	-635.7824	-635.4551	(858.76)
CPCM (G98)	-635.7821	-635.4549	(858.29)
PCM (GAMESS)	-635.7644	-635.7157	127.86
CPCM (GAMESS)	-635.7682	-635.7175	132.99

      En conclusion, les calculs montrent que de manière similaire au rhodium(III), le mécanisme concerté pour l'iridium(III) est encore plus favorisé par rapport au mécanisme dissociatif avec l'ajout des effets de solvatation.

      Comme il va l'être dit dans la partie discussion ci-après, les présents calculs ont permis de montrer que les deux aqua-ions Rh(III) et Ir(III) ont un comportement très similaire et sont tous deux caractérisés par un mécanisme d'échange d'eau concerté I énergétiquement favorisé par rapport à un mécanisme D, ce qui confirme les observations expérimentales.

      

Tabl. 4.15 : Paramètres géométriques et thermodynamiques obtenus par le calcul pour les espèces d'iridium (III)
	Symétrie		E, hartrees	DE‡, kJ/mol	d(M-O), Å	S[d(M-O)], Å	DS[d(M-O)], Å
Iridium(III) Mécanisme dissociatif
[Ir(OH2)6]3+	Th a	-559.0742		0.00	2.089; 2.089; 2.089; 2.089; 2.089; 2.089	12.5334	-
{[Ir(OH2)5(OH2)]3+}≠	Cs	-559.0185		146.10	2.101; 2.040; 2.028; 2.074; 2.074; 3.498	13.8152	1.2818
[Ir(OH2)5(OH2)]3+	Cs	-559.0197		143.03	2.106; 2.037; 2.027; 2.074; 2.074; 3.986	14.3048	1.7714
Avec le modèle SCRF
[Ir(OH2)6]3+	Th a	-559.5304		0.00	2.089; 2.089; 2.089; 2.089; 2.089; 2.089	12.5334	-
{[Ir(OH2)5(OH2)]3+}≠	Cs	-559.4327		256.27	2.100; 2.042; 2.027; 2.074; 2.074; 3.493	13.8113	1.28
[Ir(OH2)5(OH2)]3+	Cs	-559.4101		315.55	2.105; 2.039; 2.027; 2.074; 2.074; 4.019	14.3378	1.80
Avec le modèle PCM (single point seul)
[Ir(OH2)6]3+	Th a	-559.7256		0.00	-	-	-
{[Ir(OH2)5 (OH2)]3+}≠	Cs	-559.6645		160.06	-	-	-
[Ir(OH2)5(OH2)]3+	Cs	-559.6661		156.07	-	-	-
Avec le modèle CPCM (single point seul)
[Ir(OH2)6]3+	Th a	-559.7299		0.00	-	-	-
{[Ir(OH2)5(OH2)]3+}≠	Cs	-559.6738		147.11	-	-	-
[Ir(OH2)5(OH2)]3+	Cs	-559.6746		145.05	-	-	-
Iridium(III) Mécanisme concerté
[Ir(OH2)6(OH2)]3+	Cs	-635.1432		0.00	2.104; 2.071; 2.092; 2.088; 2.088; 2.076; 3.830	16.3489
{[Ir(OH2)5(OH2)2]3+}≠	C2	-635.0880		144.79	2.076; 2.076; 2.049; 2.085; 2.085; 2.737; 2.737	15.8448	-0.50
Avec le modèle SCRF
[Ir(OH2)6(OH2)]3+	Cs	-635.5437		0.00	2.104; 2.072; 2.092; 2.088; 2.088; 2.077; 3.832	16.3520
{[Ir(OH2)5(OH2)2]3+}≠	C2	-635.5293		37.78	2.076; 2.076; 2.049; 2.085; 2.085; 2.741; 2.741	15.8510	-0.50
Avec le modèle PCM (single point seul)
[Ir(OH2)6(OH2)]3+	Cs	-635.7644		0.00	-	-	-
{[Ir(OH2)5(OH2)2]3+}≠	C2	-635.7157		127.86	-	-	-
Avec le modèle CPCM (single point seul)
[Ir(OH2)6(OH2)]3+	Cs	-635.7682		0.00	-	-	-
{[Ir(OH2)5(OH2)2]3+}≠	C2	-635.7175		132.99	-	-	-
a Optimisé dans la symétrie D2h. L'ordre des distances de liaison est celui indiqué dans la figure IV.25.