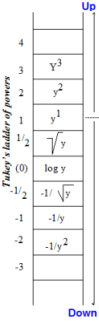 John Tukey has designed a family of power transformations (close
cousin to the box-cox transformations, but with a visual aspect useful to find the appropriate transformation to promote symmetry
and linearity relationships.
John Tukey has designed a family of power transformations (close
cousin to the box-cox transformations, but with a visual aspect useful to find the appropriate transformation to promote symmetry
and linearity relationships.| Ladder of powers | EDA |
| ? | Back |
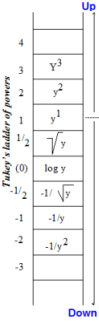 John Tukey has designed a family of power transformations (close
cousin to the box-cox transformations, but with a visual aspect useful to find the appropriate transformation to promote symmetry
and linearity relationships.
John Tukey has designed a family of power transformations (close
cousin to the box-cox transformations, but with a visual aspect useful to find the appropriate transformation to promote symmetry
and linearity relationships.
These transformations preserve order, preserve proximities and are smooth functions (not producing jumps or peaks). y1 is the untransformed (raw) variable, y0 is replaced by the logarithm that provides the appopriate transformation between the square root and the reciprocal root.
You can also use lower and higher powers as listed, as well intermediate ones, i.e. y2.5 will be stronger than y² but less than y³
The example shows the effect of the various power transformations on the symmetry of a variable.
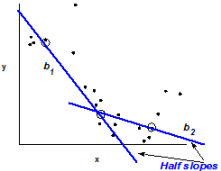 To promote linearity a visual rule of thumb has been proposed by John Tukey.
To promote linearity a visual rule of thumb has been proposed by John Tukey.
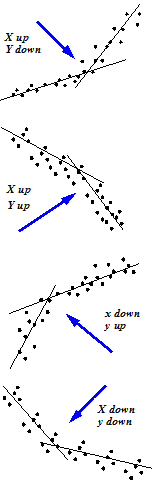 Imagine an arrow pointing into the bend of the half-lines:
To linearize the relationship (first of the four possible situations):
Imagine an arrow pointing into the bend of the half-lines:
To linearize the relationship (first of the four possible situations):
Depending on the relationship, it is enough to transform one of the variables, sometimes you will have to transform both.
Note that in all four situations the half-slopes (the slopes of the half-lines have the same sign. If the signs are different (one negative, the other positive for instance) no suitable transformation can be found!
© Copyright, Eugene Horber, U. of Geneva and FORS, 2024