Random interlacements
This page presents simulations for the phase transition associated to percolation for the vacant set of random interlacements in dimension three. The python script for these simulations is available here, along with the required companion package. You are welcome to use and modify them. Similar simulations are also available for the discrete Gaussian free field, metric graph Gaussian free field, and independent percolation.
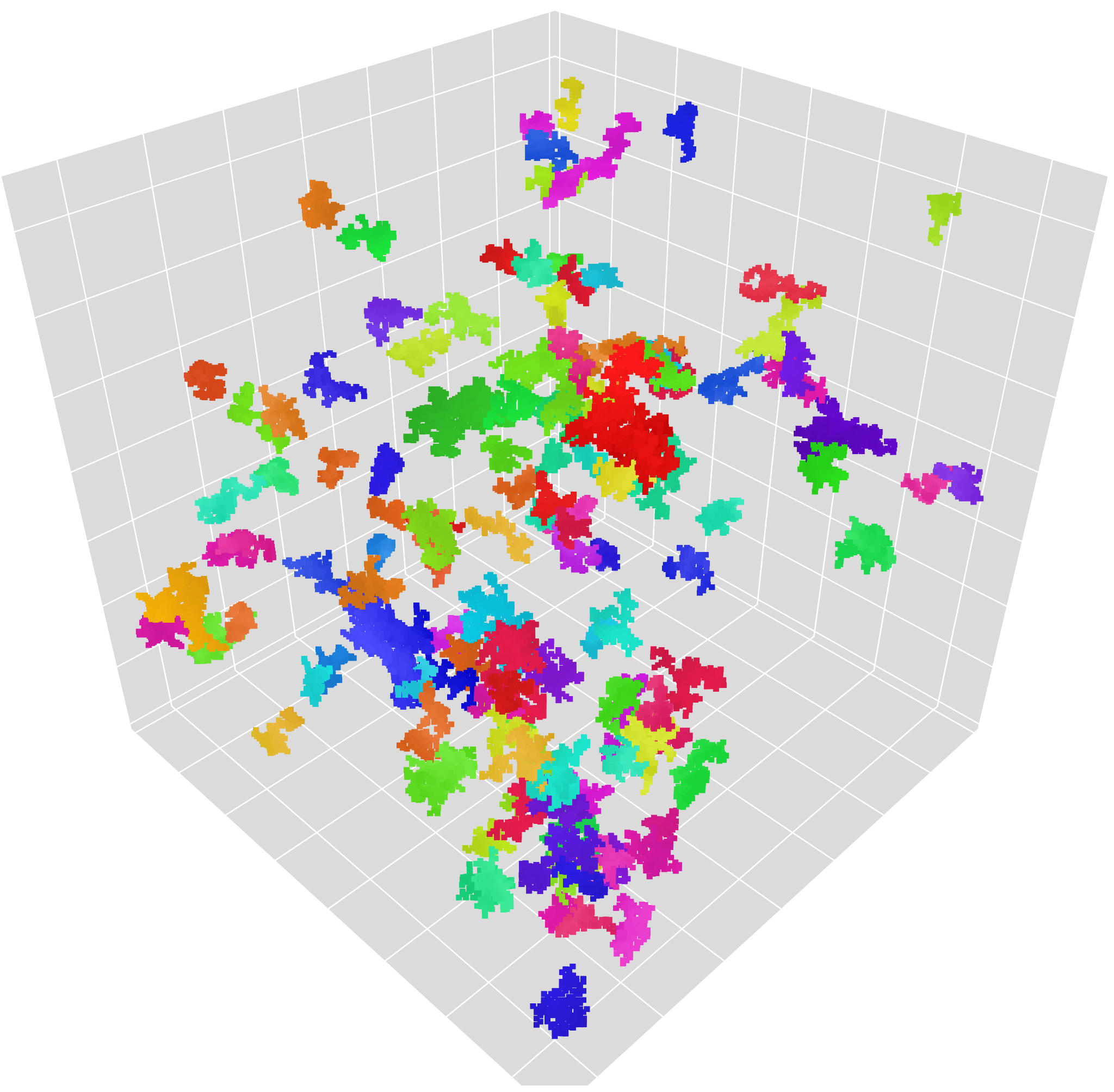
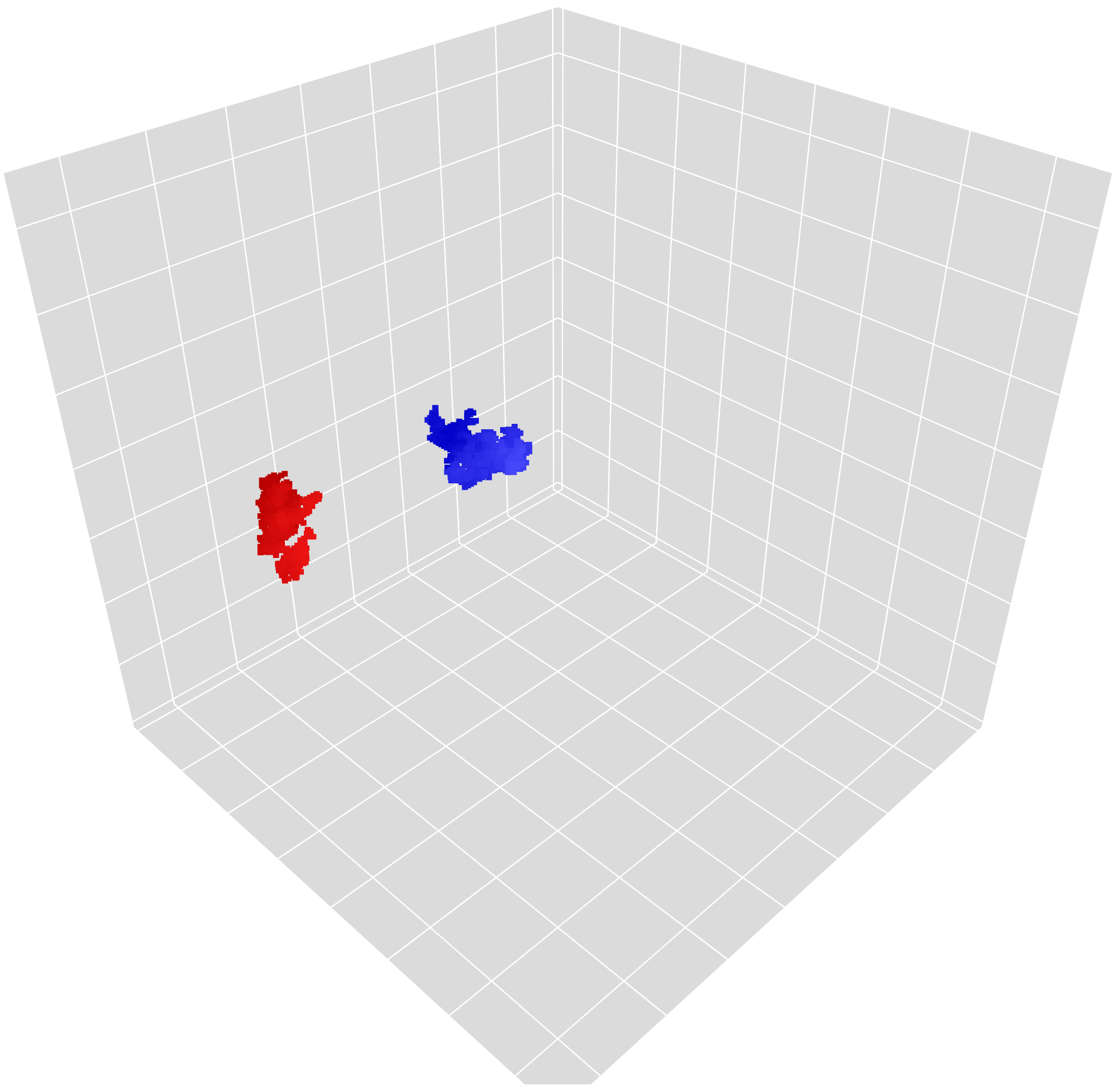
10% largest connected components
The figures below show the set of points not visited by a random walk on the three-dimensional torus with side length N at time uN3, for various values of N and u, corresponding respectively to the subcritical, critical, and supercritical regime. This is a good approximation of the vacant set of random interlacements in dimension three. Only connected components (with free boundary condition) with a cardinality exceeding 10% of the largest component are displayed. The video can be downloaded here, and a 3D representation with more points is available here (can be slow). If one is directly interested in the random walk on the torus, there are similar simulations available with periodic boundary conditions.Â
u=4.2
u=3.15
u=2.2
RW_N=200_Free_Boundary_10_Percent_Largest_1.mp4
u=4.2
u=3.15
u=2.2
RW_N=200_Free_Boundary_2_Largest_1.mp4